Teorema de Thevenins

 

Introducción

Para muchos circuitos lineales, el análisis se simplifica enormemente mediante el uso de dos técnicas de reducción de circuitos o teoremas como los teoremas de Thevenin y Norton. El teorema de Thevenin lleva el nombre de un ingeniero francés, M. L. Thevenin en 1883 y el teorema de Norton después de un científico E. L. Norton. Al usar estos teoremas, una parte grande o compleja de una red se reemplaza por un simple equivalente. Con este circuito equivalente, podemos realizar fácilmente los cálculos necesarios de la corriente, el voltaje y la potencia entregados a la carga (como lo hace el circuito original). Este tipo de aplicación garantiza seleccionar el mejor valor de resistencia a la carga. Veamos en detalle el teorema de Thevenin.

¿Por qué utilizamos el teorema de Thevenin?

En la mayoría de las aplicaciones, una red puede consistir en una carga variable elemento, mientras que otros elementos son constantes. El mejor ejemplo es nuestra toma de corriente doméstica que está conectada a diferentes electrodomésticos o cargas. Por lo tanto, si se desea, es necesario calcular el voltaje o la corriente o la potencia en cada elemento en un circuito dado para cada cambio en el componente variable. Este procedimiento repetido es de alguna manera complicado y oneroso. Dichos cálculos repetidos se evitan introduciendo un circuito equivalente para una parte fija en el circuito, de forma que el análisis del circuito con cambio en la resistencia de carga sea fácil.

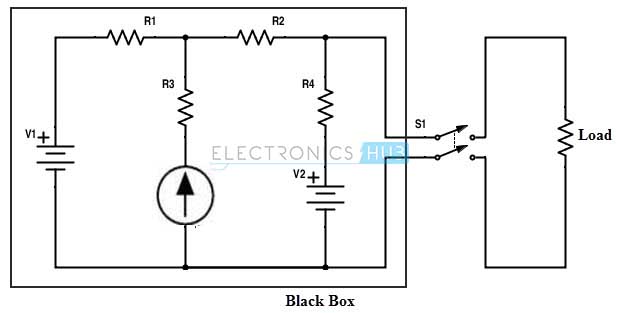
Considere el circuito DC simple anterior donde la corriente que fluye a través de la resistencia de carga puede determinarse usando diferentes técnicas como análisis de malla o nodal métodos de análisis o superposición. Supongamos que la resistencia de carga cambia a algún otro valor que no sea anterior, entonces tenemos que aplicar cualquiera de estos métodos nuevamente. Este método tedioso de aplicar la técnica de reducción para cada cambio de carga se evita reemplazando la parte fija de un circuito (dentro de la caja negra) con una fuente de tensión práctica, nada más que una manifestación del teorema de Thevenin. En la práctica, el teorema de Thevenin ayuda a encontrar la potencia máxima entregada a los altavoces que se suministran desde el amplificador en un amplificador de potencia de transistor.

Declaración del teorema de Thevenin

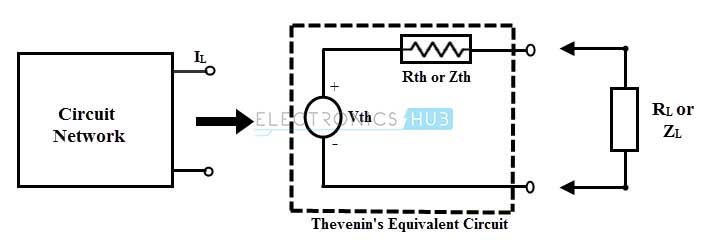
El teorema de Thevenin establece que cualquier circuito lineal de dos terminales que consta de fuentes y resistencias conectadas a una carga RL determinada puede ser reemplazado por un circuito equivalente que consta de una única fuente de magnitud de tensión Vth con una resistencia en serie Rth en el terminal de RL.

La siguiente figura muestra el modelo de Thevenin de dos redes de terminales donde la corriente a través de la carga es la misma, por lo tanto, estos dos circuitos son equivalentes entre sí.

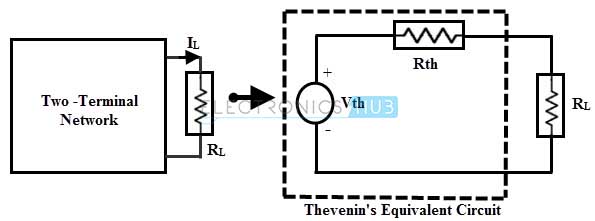
Similar a los circuitos de CC, este método se puede aplicar a los circuitos de CA que consisten en elementos lineales como resistencias, inductores, condensadores. Al igual que la resistencia equivalente devinin, la impedancia equivalente devinin se obtiene reemplazando todas las fuentes de voltaje por sus impedancias internas.

En los circuitos de CA, el teorema de Thevenin puede establecerse como cualquier circuito terminal lineal bilateral que consta de elementos lineales y activos las fuentes conectadas a través del terminal de ZL pueden reemplazarse por una única fuente de voltaje equivalente de V con una sola impedancia Z a través de los dos terminales de ZL.

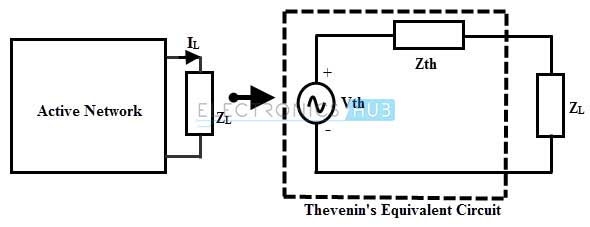
Pasos para analizar el teorema de Thevenin

Los siguientes son th e pasos para simplificar el circuito de modo que la corriente de carga se determine usando el teorema de Thevenin.

1. Considere el circuito dado y desconecte la resistencia de carga RL (impedancia de carga ZL) o la resistencia de derivación (impedancia de derivación en el circuito de CA) a través de la cual se calculará el flujo de corriente.

2. Determine el voltaje de circuito abierto Vth a través de la carga después de desconectar RL. Para encontrar Vth, uno puede aplicar cualquier método de técnicas de reducción de circuitos disponibles como análisis de malla, método de voltaje nodal, superposición, etc. O simplemente, podemos medir el voltaje en los terminales de carga usando un voltímetro.

3. Redibuja el circuito reemplazando todas las fuentes con sus resistencias internas (impedancias internas en el caso del circuito de CA) y asegúrate de que las fuentes de voltaje estén en cortocircuito y que las fuentes de corriente estén en circuito abierto (para las fuentes ideales).

4. Calcule la resistencia total Rth (o Zth) que existe entre los terminales de carga.

5. Inserte esta resistencia equivalente Rth (o Zth) en serie con la tensión Vth y este circuito se conoce como el circuito equivalente de Thevenin.

6. Ahora reconecte la resistencia de carga (impedancia de carga ZL) a través de los terminales de carga y calcule la corriente, el voltaje y la potencia de la carga mediante cálculos simples.

En el circuito DC,

Carga de corriente,

IL = Vth/(RL + Rth)

Voltaje en la carga,

VL = RL × Vth/(RL + Rth)

Potencia disipada en la resistencia de carga,

PL = RL × IL2

En caso de circuito de corriente de carga,

IL1 = Vth/(ZL ​​+ Zth)

El voltaje acorss la carga,

VL = ZL × Vth/(ZL ​​+ Zth)

Potencia disipada en la resistencia de carga, PL = ZL × IL12

Ejemplo de búsqueda de un circuito equivalente en el circuito de CC

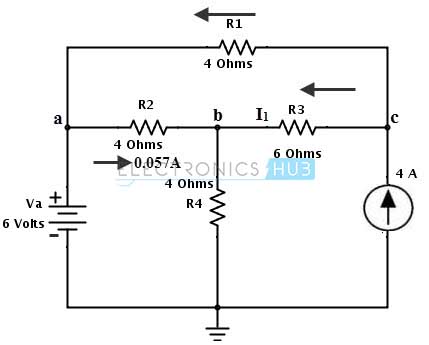
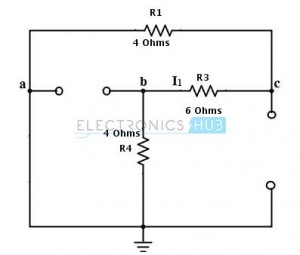
Considere el circuito de CC que se muestra a continuación. Vamos a encontrar la corriente a través de la resistencia R2 = RL = 2 ohmios (conectada entre las terminales a y b) aplicando el teorema de Thevenin.

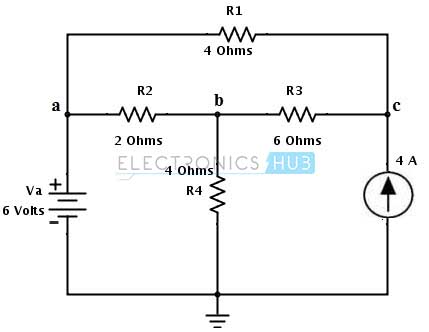
1. Elimine la resistencia de carga R2 o RL y adopte la dirección de la ruta cerrada hacia el punto C.

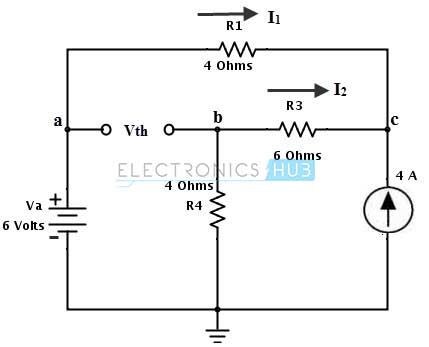
2. Aplique el análisis nodal en el nodo C para calcular el voltaje de thevenin Vth.

Aplicando KCL en el nodo C obtenemos

4 + I1 + I2 = 0

4 + (6-Vc)/4 + (0-Vc)/10 = 0

Vc = 15.714 voltios

Luego, las corrientes en cada rama se pueden determinar como

I1 = Va-Vc/4

= 6-15.714/4

= 2.0715 Amps

I2 = 0-Vc/10

=-15.714/10

=-1.571 Amps

El símbolo negativo indica que la corriente está fluyendo desde el nodo C a su punto respectivo (como & # 8216; a ’ y puntos de tierra para I1 e I2 respectivamente).

Redibujando el circuito con estas corrientes y aplicando KVL, el voltaje a través del terminal ab se determina como,

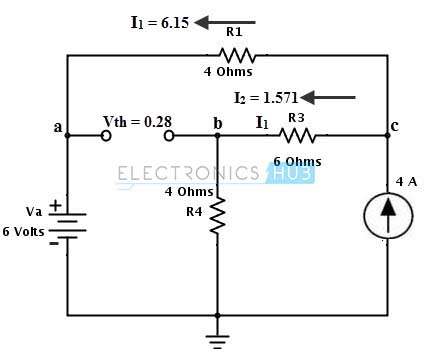
Vth = Va-Vb (con respecto a los terminales de tierra)

= Va-(I2 × R4)

= 6-(1.571 × 4)

= 0.28 voltios

3. Siguiente El paso es reemplazar todas las fuentes con sus fuentes internas. Considere que la fuente de voltaje es una fuente ideal, por lo que la resistencia interna es cero, por lo tanto, está cortocircuitada y la fuente de corriente es una fuente de corriente ideal, por lo tanto tiene resistencia infinita. En ese momento, se muestra el circuito de resistencia equivalente de Thevenin.

4. A continuación, tenemos que encontrar la resistencia equivalente de Thevenin Rth mirando los terminales a y b (terminales de carga).

Rth = [(R1 + R3) × R4]/[(R1 + R3) + R4] (resistencias paralelas)

= 10 × 4/10 + 4

= 2.85 Ohms

5. Al colocar la fuente de tensión calculada anteriormente en serie con una resistencia equivalente, se forma el circuito equivalente de Thevenin como se muestra en la figura siguiente.

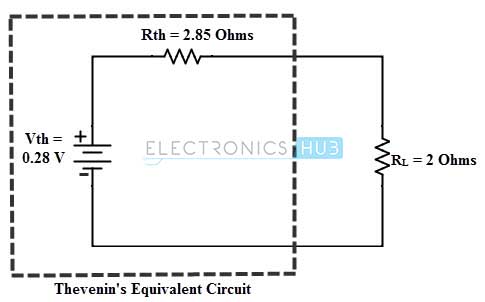
Al volver a conectar la resistencia de carga en los terminales a y b, calculamos la corriente que fluye a través de la carga como

IL = Vth/(Rth + RL)

= 0.28/(2.85 + 2)

= 0.057 Amps

Y debajo de la figura se muestra el circuito original donde se indica la corriente a través de la resistencia de carga.

También podemos encontrar las corrientes a través de la carga cambiando el valor de la resistencia de carga como

Cuando RL = 8 ohmios

IL = 0.28/(2.85 + 8)

= 0.02Amps

Cuando RL = 12 ohmios

= 0.28/(2.85 + 12)

= 0.01 Amps

Volver arriba

Ejemplo de búsqueda de circuito equivalente en el circuito de CA

Considere el siguiente circuito de CA al cual vamos a encontrar la corriente a través de la impedancia 4+ 4j ohm usando el teorema devenin.

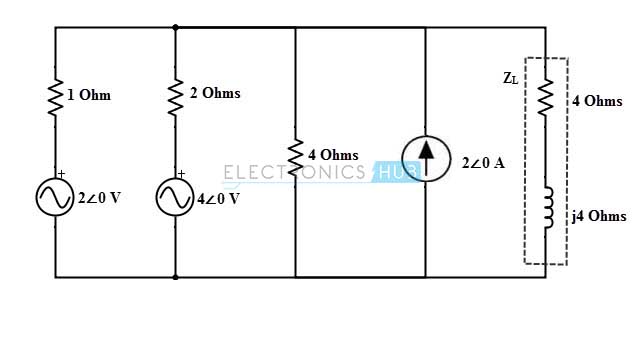
En el circuito anterior, la fuente de corriente de 2∠0 en paralelo con la resistencia de 4 ohm. Y, por lo tanto, esto se puede convertir en un voltaje fuente 8∠0 con una resistencia en serie de 4 ohmios como se muestra en la figura.

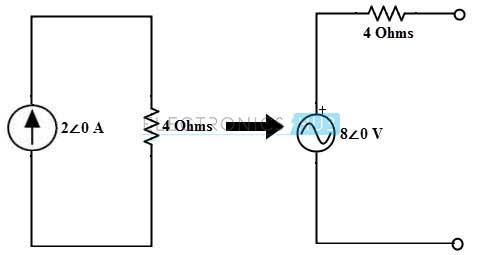
Después de hacer el cambio anterior, el circuito se vuelve a dibujar desconecte los terminales de carga como se muestra en la figura a continuación.

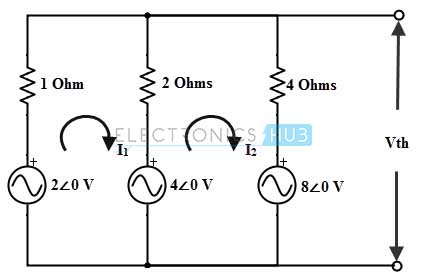
Suponga las corrientes de malla como se muestra en el diagrama modificado y la ecuación KVL de la malla son

2∠0-I1-2 (I1-I2)-4∠0 = 0

-3I1 + 2I2 = 2 … …. (1)

Para malla 2

4∠0-2 (I2-I1)-4I2-8∠0 = 0

2I1-6I2 = 4 … …. (2)

Al resolver las dos ecuaciones anteriores, obtenemos

I2 =-1.142∠0 A

Por lo tanto,

Vth = 8∠0-4 × (1.142∠0)

= 3.43∠0 V

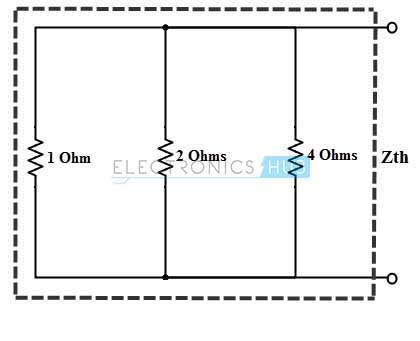
La impedancia equivalente,

Zth = 1/(1 + (1/2) + (1/4))

= 0.574 ∠0

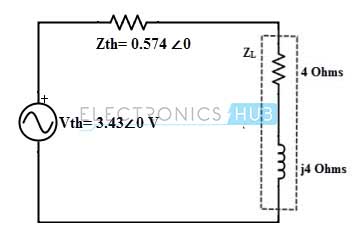
Por lo tanto, se da la corriente a través de la impedancia 2 + 2j como,

IAB = Vth/Zth + ZL

= 3.43∠0/(0.574 ∠0 + 4 + 4j)

= 3.43∠0/(6.07 ∠41.17)

= 0.56∠-41.17 A

Limitaciones o f Teorema de Thevinen

• Si el circuito consta de elementos no lineales, este teorema no es aplicable.

• También a las redes unilaterales no es aplicable.

• No debe haber un acoplamiento magnético entre la carga y el circuito que deba reemplazarse con el equivalente de thevinen.

• No debe haber fuentes controladas en el lado de la carga que se controlen con cuidado desde otras partes de la red.