Contenido
- 1 Capacitancia
- 2 Autocapacitancia
- 3 Capacitancia parásita
- 4 Capacitancia de sistemas simples
- 5 Carga en un condensador
- 6 Condensador de placas paralelas
- 7 Ejemplo de capacitancia No1
- 8 Carga y amp; Descarga de un condensador
- 9 Ejemplo de carga del condensador No2
- 10 Corriente a través de un condensador
- 11 Unidad de capacitancia (Farad)
- 12 Subunidades del Farad
- 13 Energía en un condensador
- 14 Artículos relacionados en la web
Capacitancia
La capacitancia de un condensador se define como la capacidad de un condensador para almacenar la carga eléctrica máxima (Q) en su cuerpo. Aquí la carga se almacena en forma de energía electrostática. La capacitancia se mide en las unidades basicSI, es decir, Farads. Estas unidades pueden estar en micro-farads, nano-farads, pico-farads o en faradios. La expresión de la capacitancia viene dada por,
C = Q/V = εA/d = ε0 εr A/d
En la ecuación anterior
C es la capacitancia,
Q es la carga,
V es la diferencia de potencial entre las placas,
A es el área entre las placas,
d es la distancia entre las placas.
ε permitividad del dieléctrico
ε0 espacio libre de permitividad
εr permitividad relativa del espacio libre
Autocapacitancia
La propiedad de autocapacitancia está relacionada con los condensadores, especialmente con los conductores aislados. Como su nombre indica, la capacitancia es propiedad de un conductor aislado para elevar su diferencia de potencial a un voltio. Por lo general, los conductores normales tendrán capacidad mutua. Esto también se mide en las unidades SI, es decir, Faradios.
La autocapacitancia de una esfera conductora que tiene el radio ‘R’ está dada por,
C = 4 πɛoR
Los valores de autocapacitancia de algunos dispositivos estándar se dan a continuación.
- Para la placa superior de un generador van de Graff que tiene un radio de 20 cm, la autocapacidad es de 22.24 pF.
- Para el planeta, la autocapacidad del planeta es 710 uF.
Capacitancia parásita
La capacitancia parásita es la capacidad indeseada. los condensadores introducen algo de capacitancia en el circuito. Pero los componentes como resistencias, inductores, incluso cable tendrán algo de capacitancia. Esto se llama capacitancia parásita. Generalmente a altas frecuencias, esto introducirá ruido en el circuito. Esta capacitancia indeseada es pequeña a menos que los conductores estén muy juntos para distancias largas o para un área grande.
La capacitancia parásita no se puede eliminar por completo, pero se puede reducir. Los diseñadores de circuitos deben tener en cuenta la capacitancia parásita al diseñar el circuito. La separación entre los componentes y las líneas debe mantenerse para reducir la capacitancia no deseada.
También se mide en unidades SI, es decir, Faradios.
Ejemplos son capacitancia entre los giros de la bobina, capacitancia entre dos conductores adyacentes.
Capacitancia de sistemas simples
El cálculo de la capacitancia no es más que resolver el teorema de Laplace ∇ 2φ = 0 con un potencial constante en la superficie de un condensador. Los valores de capacitancia y las ecuaciones para algunos sistemas simples se dan a continuación.
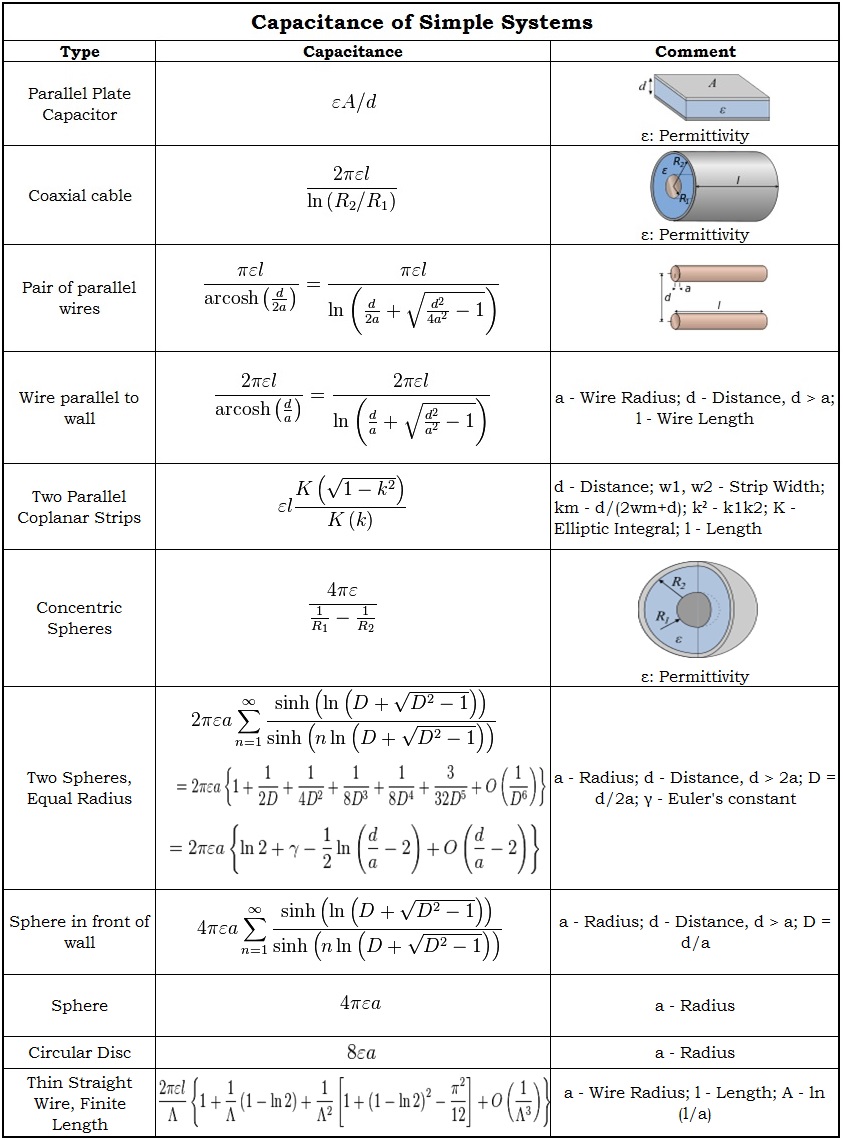
Carga en un condensador
La capacidad de un condensador para almacenar carga máxima (Q) en sus placas de metal se llama su valor de capacitancia (C). La polaridad de la carga almacenada puede ser negativa o positiva. Como la carga positiva (+ ve) en una placa y la carga negativa (-ve) en otra placa del condensador. Las expresiones de carga, capacitancia y voltaje se dan a continuación.
C = Q/V, Q = CV, V = Q/C
Por lo tanto, la carga de un condensador es directamente proporcional a su valor de capacitancia y la diferencia de potencial entre las placas de un condensador. La carga se mide en culombios.
Un culombio:
Un culombio de la carga en un condensador se puede definir como un faradio de capacitancia entre dos conductores que operan con un voltaje de un voltio.
Con aire como su dieléctrico
La carga ‘Q’ almacenada en el capacitor con capacitancia C, potencial diferencia ‘V’ y el aire como su dieléctrico está dado por,
Q = CV = (ε × (A × V))/d
Con un sólido como su dieléctrico
La carga ‘Q’ de un condensador que tiene un sólido como su dieléctrico está dada por,
Q = CV = (ε0 × εr × (A × V))/d
Aquí
ε0 es el permiso ivity del espacio libre,
εr es la permitividad relativa del material dieléctrico y
es la permitividad del material dieléctrico.
De los dos casos anteriores podemos observar
La carga de un condensador es directamente proporcional al área de las placas, permitividad del material dieléctrico entre las placas y es inversamente proporcional a la distancia de separación entre las placas.
Así más grande es el área de las placas más la carga y mayor la distancia de separación entre las placas menor la carga en el condensador.
Condensador de placas paralelas
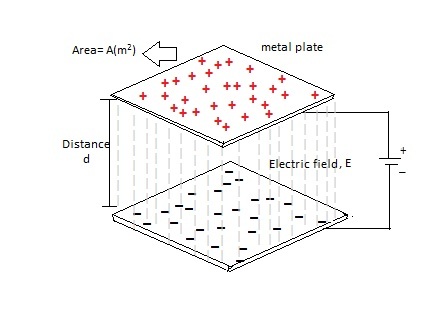
Figura 1. circuito condensador de placas paralelo.
La figura de arriba muestra el circuito del condensador de placas paralelas. Como sabemos, la capacidad es directamente proporcional al área de las placas (A) e inversamente proporcional a la distancia de separación (d) entre dos placas de metal. El valor de capacitancia de un condensador de placas paralelas está dado por,
C = k ε0A/d
Aquí k es la constante dieléctrica, y ε0 es la permitividad del espacio libre y es igual a 8.854 X 10-12 F/m. La constante dieléctrica (k) es un parámetro relacionado con el material dieléctrico que aumenta la capacitancia en relación con el aire. El área de superficie más grande de las placas es mayor que el valor de capacitancia y la distancia de separación más grande es la capacidad. Se muestra un ejemplo más para el circuito condensador de placas paralelas en la figura siguiente.
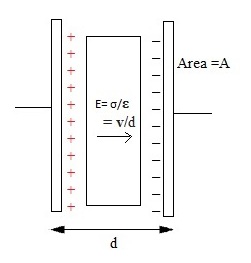
Figura 2. Condensador de placas paralelas.
Ejemplo de capacitancia No1
Ahora lo haremos calcule la capacitancia de un condensador de placas paralelas en pico farads que tiene el área de superficie de las placas es de 200 cm2 y están separadas por la distancia de 0,4 cm, y el aire como su material dieléctrico.
sabe que la ecuación para la capacitancia de un capacitor de placa paralela es,
C = εA/d
Aquí ε = 8.854 X 10-12F/m
A = 200 cm2 = 0.02 m2
D = 0.4 cm = 0.004m
Ahora sustituimos estos valores en la ecuación anterior,
C = 8.854 X 10-12 * (0.02 m2/0.004m) = 44.27 pF
Aquí la capacitancia de un condensador de placa paralela es 44,27 pF
Carga y amp; Descarga de un condensador
El siguiente circuito se usa para explicar las características de carga y descarga de un condensador. Supongamos que el condensador, que se muestra en el circuito, está completamente descargado. En este circuito, el valor del condensador es 100 uF y la tensión de alimentación aplicada a este circuito es de 12 V.
Ahora el interruptor que está conectado al condensador en el circuito se mueve al punto A. A continuación, el condensador comienza a cargarse con la corriente de carga (i) y también este condensador está completamente cargado. La tensión de carga en el condensador es igual a la tensión de alimentación cuando el condensador está completamente cargado, es decir VS = VC = 12V. Cuando el condensador está completamente cargado significa que el capacitor mantiene la carga de voltaje constante incluso si la tensión de alimentación se desconecta del circuito.
En el caso de condensadores ideales, la carga permanece constante en el condensador, pero en el caso de condensadores generales, el condensador completamente cargado se descarga lentamente debido a su corriente de fuga.

Figura: Cargando y descargando el circuito del condensador
Cuando el interruptor se mueve a la posición B, entonces el condensador se descarga lentamente encendiendo la lámpara que está conectada en el circuito. Finalmente está completamente descargado a cero. La lámpara brilla intensamente inicialmente cuando el condensador está completamente cargado, pero el brillo de la lámpara disminuye a medida que disminuye la carga en el condensador.
Ejemplo de carga del condensador No2
Ahora calculemos el carga de un condensador en el circuito anterior, sabemos que la ecuación para la carga de un condensador es
Q = CV
Aquí, C = 100uF
V = 12V
Ahora sustituimos estos valores en la ecuación anterior,
Q = 100uF * 12V = 1.2mC
Por lo tanto, la carga del condensador en el circuito anterior es de 1,2 mC.
Corriente a través de un condensador
La corriente (i) que fluye por cualquier circuito eléctrico es la tasa de carga ( Q) que fluye a través de él con respecto al tiempo. Pero la carga de un condensador es directamente proporcional al voltaje aplicado a través de él. La relación entre la carga, la corriente y la tensión de un condensador se da en la siguiente ecuación.
I (t) = d Q (t)/dt = C dV (t)/dt
Sabemos que
Q = CV
V = Q/C
V (t) = Q (t)/C
Q (t) = CV (t)
La relación de corriente a tensión está dada por, I ( t) = C dV (t)/dt
De esta relación observamos que la corriente que fluye a través del condensador en el circuito es el producto de la capacitancia y la tasa de cambio de voltaje aplicada al circuito. La corriente que fluye a través del condensador es directamente proporcional a la capacitancia de un condensador y la tasa de voltaje.
Mayor es la corriente, mayor es la capacitancia del circuito y mayor es el voltaje aplicado, mayor es la corriente que fluye el circuito. Si el voltaje es constante, la carga también es constante. Por lo tanto, no hay flujo de carga. Por lo tanto, la corriente que fluye a través del circuito se convertirá en cero.
Unidad de capacitancia (Farad)
Josiah Latimer Clark en el año de 1861 utilizó por primera vez el términoFarad. Farad es una unidad estándar de la capacitancia. Esta es una unidad extremadamente grande para la capacitancia.
Un faradio de capacitancia se define como la capacitancia con un culombio de carga que opera a la tensión de un voltio.
C = Q/V
1Farad = 1Coluomb/1Volt
Ahora los condensadores están disponibles con grandes valores de capacitancia de cientos de faradios. Estos condensadores con altos valores de capacitancia se llaman «supercondensadores». Estos condensadores están utilizando una gran área de superficie para entregar alta energía porque tienen altos valores de capacitancia.
A bajo voltaje, los supercondensadores tienen la capacidad de almacenar alta energía con altos valores de capacitancia. Estos supercondensadores de alta energía se utilizan en dispositivos portátiles portátiles para reemplazar condensadores de tipo litio grandes, pesados y costosos, ya que almacenan alta energía, como las baterías. Estos condensadores también se usan en sistemas de audio y video en vehículos al reemplazar las baterías altas.
Subunidades del Farad
La unidad estándar de capacitancia es farad. Pero esta es generalmente una unidad grande para la medición de capacitancia. Este farad tiene algunas unidades secundarias; son micro-farads (uF), nano-farads (nF) y pico-farads (pF).
La relación entre estas todas las subunidades con farad es
1micro-Farad (uF) = (1/1000000) F = 10-6 F
1nano-Farad (uF) = (1/1000000000) F = 10-9 F
1pico-Farad (uF) = (1/1000000000000) F = 10-12 F
Ahora veremos algunas conversiones entre las subunidades de capacitancia,
(i) conversión de 33pF a nF = & gt; 33pF = 0.033nF
(ii) conversión de 22nF a uF = & gt; 22nF = 0.022uF
(iii) conversión de 11uF a F = & gt; 11uF = 0.11F
Energía en un condensador
La energía es la cantidad de trabajo contra el campo electrostático para cargar completamente el condensador. En el condensador en la etapa inicial de carga, la carga Q se transfiere entre las placas de una placa a otra. Esta carga ya sea + Q o-Q se intercambia entre dos placas de un condensador. Después de la transformación de alguna carga, se forma un campo eléctrico entre las placas, en ese caso necesitamos un trabajo adicional para cargar el condensador completamente. Este trabajo adicional se denomina energía almacenada en un condensador. La energía se mide en las unidades de Joules (J). Ahora vemos las ecuaciones para esta energía y trabajo.
dW = V dQ
dW = (Q/C) dQ
Después de la integración de la ecuación anterior,
W = Q2/2C
W = (CV) 2/2C
W = CV2/2 Joules
Finalmente obtenemos la energía almacenada en un condensador es
Energy (W) = CV2/2 Joules
Ahora calculamos la energía almacenada en un condensador de capacitancia de 200 uF que opera con voltaje de 12V.
W = CV2/2
W = (200 × 10-6 × 122)/2 = 14.4 m J