Las olas son omnipresentes por naturaleza y transfieren la energía o la información de la fuente a su destino. La ola es una función del espacio y el tiempo. Un tipo de onda exótica es la onda electromagnética cuya existencia es establecida por el profesor Heinrich Hertz, pero el mismo Maxwell predijo la existencia de ondas electromagnéticas.
Estas ondas pueden viajar a través de un vacío o ningún medio. Estos son diferentes de las ondas mecánicas como las ondas de sonido que pueden viajar o transportar su energía a través de un medio de material.
Así, a diferencia de las ondas mecánicas, las ondas electromagnéticas pueden viajar a través del vacío. Los ejemplos típicos de las ondas electromagnéticas son ondas de luz visibles, ondas de radio, haces de radar y señales de TV. El tema de ondas electromagnéticas es un fenómeno compuesto de campos eléctricos y magnéticos.
Contenido
Uniform Plane Wave y Ecuación de onda
La comprensión básica de la propagación de ondas electromagnéticas en el medio es proporcionada por el concepto básico de onda plana uniforme. La onda plana uniforme es un concepto fundamental en electromagnetismo y es la solución más simple a la ecuación de Maxwell para campos variables en el tiempo en un medio homogéneo no unido.
Aunque en la práctica no existe un medio tan común como homogéneo, el concepto fundamental de onda plana uniforme es muy útil para el conocimiento de las ondas electromagnéticas. Además, la solución uniforme de onda plana es bastante útil y adecuada prácticamente en muchos problemas.
En algunos casos donde los medios tienen dimensiones físicas mucho más grandes que la longitud de onda, la solución se aproxima mucho a la solución de onda uniforme.
Considere un medio homogéneo, isotrópico e ilimitado que no consista en ninguna fuente eléctrica o magnética. En tal caso, la permeabilidad media μ y la permitividad є son constantes en todo el medio. Dado que el medio es de origen libre y, por lo tanto, no hay cargos gratuitos en el medio. Las ecuaciones de Maxwell se dan como
∇.D~ = 0
∇. B̅ = 0
∇ × E̅ =-∂B̅/∂t
∇ × H̅ = J̅ + ∂D̅/∂t
De las relaciones constitutivas,
B̅ = μ H̅
D̅ = є E̅
J̅ = σ E̅
The la permeabilidad μ y la permitividad є son constantes como una función del tiempo y el espacio debido al medio homogéneo y que no varía en el tiempo. Por lo tanto, las ecuaciones de Maxwell se convierten en
∇. B ̅ = ∇. (μ H ̅) = μ ∇. H ̅ = 0
∇. H ̅ = 0………. (1)
∇. D ̅ = ∇. (є E ̅) = є ∇. E ̅ = 0
∇. E ̅ = 0………. (2)
∇ × E ̅ =-∂ (μ H)/∂t
∇ × E ̅ =-μ ∂ H ̅/∂t………. (3)
∇ × H ̅ = ∂ (є E ̅)/∂t
∇ × H ̅ = σ E ̅ + є ̅ E ̅/∂t………. (4)
En lo anterior, ∇ indica la diferenciación con respecto al espacio, mientras que ∂/∂t indica diferenciación con respecto al tiempo. De las ecuaciones 3 y 4 anteriores, podemos decir que la derivada temporal del campo magnético se relaciona con la derivada espacial del campo eléctrico y también, la derivada temporal del campo eléctrico se relaciona con la derivada espacial del campo eléctrico.
Por lo tanto, a partir de estas dos ecuaciones se debe tener en cuenta que un campo magnético variable en el tiempo no puede existir sin el correspondiente campo eléctrico y magnético. Por lo tanto, tanto los campos magnéticos como los eléctricos deben coexistir para producir los campos variables en el tiempo.
Para estos campos variables en el tiempo, no podemos obtener solo campos magnéticos o solo eléctricos variables en el tiempo. Pero en el caso de campos invariantes en el tiempo, como campos electrostáticos y magnetostáticos, pueden existir uno sin el otro.
Tomando el curl de la ecuación 3 y 4, obtenemos
∇ × ∇ × E ̅ =-μ ∇ × ∂ H ̅/∂t
∇ × ∇ × H ̅ = ∇ × (σ E ̅ ) + ∇ (є ̅ E ̅/∂t)
Ambos ∇ y ∂/∂t son independientes entre sí, por lo que los operadores pueden intercambiarse como
∇ × ∇ × E ̅ =-μ × ∂ (∇ × H ̅)/∂t
∇ × ∇ × H ̅ = σ (∇ × E ̅) + є × ∂ (∇ × E ̅)/∂t
Sustituyendo el (∇ × H) y (∇ × E) valores de 3 y 4 ecuaciones, obtenemos
∇ × ∇ × E ̅ =-μ × ∂/∂t ( σ E ̅ + є ̅ E ̅/∂t)
∇ × ∇ × E ̅ =-μ σ × ∂ E ̅/∂t-μ є ∂2 E ̅/∂t2)
Del mismo modo
∇ × ∇ × H ̅ = σ-μ ∂ H ̅/∂t) + є × ∂/∂t (-μ ∂ H ̅/∂t)
=-μ σ (∂ H) ̅/∂t)-μ є (∂2 H ̅/∂t2)
Usando la identidad del vector ∇ × ∇ × A = ∇ (∇. A)-∇2 A, donde A es el vector arbitrario, las ecuaciones anteriores pueden escribirse como
∇ (∇.E ̅)-∇2E ̅ =-μ × ∂/∂t (σ E ̅ + є ̅ E ̅/∂t)
∇ (∇.H ̅)-∇2 H ̅ =-μ σ × ∂ E ̅/∂t-μ є (E2 E ̅/∂t2)
Pero las ecuaciones 1 y 2, (∇. E ̅) = 0 y (∇.H ̅) = 0 luego
-∇2 E ̅ =-μ σ × ∂ E ̅/∂t-μ є (∂2 E ̅/∂t2)
∇2 E ̅ = μ σ × ∂ E ̅/∂t + μ є (∂2) ̅/∂t2)…… (5)
Esta es la ecuación de onda para el campo eléctrico E ̅ para un medio. Y de forma similar
-∇2 H ̅ =-μ σ (∂ H ̅/∂t)-μ є (∂2 H ̅/∂t2)
∇2 H ̅ = μ σ (∂ H ̅/∂t) + μ є (∂2 H ̅/∂t2)…… (6)
Esta es la ecuación de onda para el campo magnético de un medio.
Las ecuaciones anteriores de 5 y 6 son las ecuaciones de onda y sus soluciones representan la onda fenómeno en el espacio tridimensional. Finalmente, concluimos que para la existencia de campos variables en el tiempo en un medio homogéneo e ilimitado, deben existir en forma de onda.
Además, deben existir campos eléctricos y magnéticos juntos. Así es como se llama a este fenómeno como una onda electromagnética.
Pero para el espacio libre, J = 0, σ = 0, є = єo y μ = μo. Sustituyendo estos valores en 5 y 6 ecuaciones obtenemos
∇2 E ̅ = μo єo (∂2 E ̅/2t)
∇2 H ̅ = μo єo (∂2 H ̅/∂t2)
Las ondas EM viajan en la dirección del plano Z, de ahí que ambos vectores E ̅ y H ̅ son independientes de x y y. Por lo tanto, los vectores E ̅ y H ̅ son la función de z y t. Por lo tanto, las ecuaciones anteriores se convierten en
∂2 E ̅/∂2 = μo єo (∂2 E ̅t2)
Al reordenar los términos, obtenemos
∂2 E ̅t2 = (1/μo єo) (∂2E ̅/∂z2)
De acuerdo con los resultados en física,
Velocidad de la luz v = (1/√ (μo єo)) = 3 × 108 m/s
v2 = (1/μ є)
Sustituyendo en la ecuación anterior obtenemos
∂2E ̅/2t2 = v2 (∂2 E ̅/∂z2 )
Similarmente ∂2H ̅ = v2 (∂2H ̅ /2t)
Propagación de onda plana
Electromagnética las ondas en un medio se caracterizan por parámetros eléctricos como permeabilidad, permitividad y conductividad. Las ondas EM están asociadas con campos eléctricos y magnéticos que son perpendiculares entre sí y perpendiculares a la dirección de propagación.
Generalmente, la dirección de propagación debe tomarse a lo largo del eje Z. La velocidad de propagación para todas las ondas EM en un espacio libre es igual a la velocidad de la luz, es decir, 3 × 108 m/s. La dirección de propagación es normal al plano formado por los vectores de campo magnético y eléctrico.
Y la fase de estos campos es independiente de los ejes xey, por lo que no existe variación de fase sobre las superficies planas ortogonales a la dirección de la propagación.
Las ondas que son uniformes en magnitud y dirección en los planos de una orientación establecida se llaman ondas planas. Las magnitudes de los campos de onda EM (campo eléctrico y magnético) son constantes en xy-el plano y la superficie de la fase constante forman un plano paralelo al plano xy y, por lo tanto, estas ondas se denominan ondas planas.
Según las ecuaciones rizadas de Maxwell, el campo eléctrico oscilante produce un flujo magnético que oscila para crear el campo eléctrico. Esta interacción entre estos dos campos hace que se almacene la energía, por lo tanto lleva la energía.
Las propiedades importantes de las ondas son amplitud, fase o frecuencia, lo que permite que las ondas transporten la información desde el origen hasta el destino.
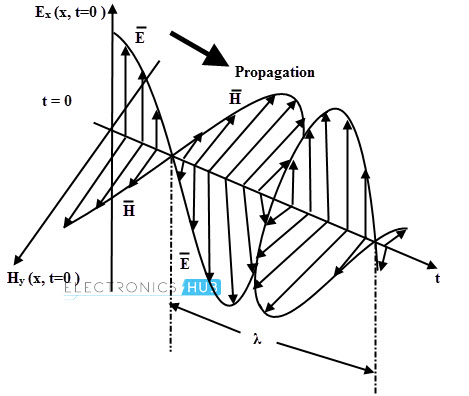
En particular, las ondas planas uniformes son ondas EM cuyo campo eléctrico es la función de xy el tiempo t e independiente de los ejes yy z.
Estas ondas son básicamente ondas TEM (ondas EM transversales) en las que los campos E y H siempre tienen magnitudes constantes y están en fase de tiempo. La potencia transmitida por los campos E y H es en la dirección de propagación.
Polarización de onda EM
Es importante saber que la dirección del vector del campo eléctrico cambia con el tiempo para una onda plana uniforme que decide la polarización de la onda. Esto se debe a que algunas aplicaciones solo pueden recibir o transmitir un tipo de ondas electromagnéticas polarizadas y el mejor ejemplo es que las antenas diferentes en aplicaciones de RF están diseñadas para un tipo de onda polarizada.
En una onda EM de plano, la eléctrica el campo oscila en el plano xz mientras que el campo magnético oscila en el plano yz. Por lo tanto, corresponde a una onda polarizada. El plano en el que oscila el campo eléctrico se define como el plano de polarización.
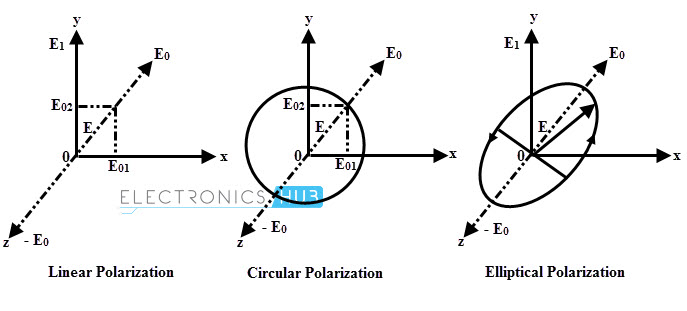
La polarización no es más que una forma en la que un campo eléctrico varía con la magnitud y la dirección. La polarización puede ser lineal, circular o polarización elíptica. Consideremos que E ̅x y E ̅y son los campos eléctricos dirigidos a lo largo de los ejes xy y, respectivamente, y también E ̅ es el resultado de E ̅x y E ̅y.
Polarización lineal
Si el campo eléctrico de una onda EM es paralelo al eje x, entonces se dice que la onda está x polarizada linealmente. Una antena de cable recta paralela al eje x podría generar este tipo de onda polarizada. De forma similar, las ondas polarizadas y se generan y definen a lo largo del eje y.
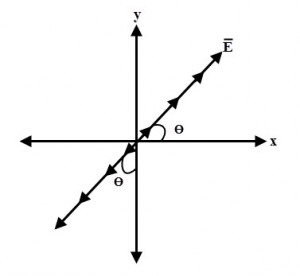
Supongamos que E ̅ tiene componentes E ̅x y E ̅y que están en fase y tienen diferentes magnitudes. Las magnitudes de E ̅x y E ̅y alcanzan sus valores máximo y mínimo simultáneamente cuando E ̅x y E ̅y están en fase. Entonces, en cualquier punto del eje z positivo, la relación de magnitudes de ambas componentes es constante.
Por lo tanto, la dirección del campo eléctrico resultante E ̅ depende de las magnitudes relativas de E ̅x y E ̅y. Por lo tanto, el ángulo formado por E ̅ con el eje x viene dado por
Θ = tan-1 Ey/Ex
donde Ey y Ex son las magnitudes de E ̅y y E ̅x, respectivamente.
Con respecto al tiempo, este ángulo es constante y, por lo tanto, se dice que la onda está polarizada linealmente. Por lo tanto, la polarización del plano uniforme que se propaga en una dirección z es lineal cuando E ̅x y E ̅y están en fase con magnitudes desiguales o iguales.
Polarización circular
Si los dos planos E ̅y y E ̅x (que están ortogonalmente polarizados) son de igual amplitud pero tiene una diferencia de fase de 90 grados entre ellos, entonces la onda resultante está polarizada circularmente. En tal caso en cualquier instante de tiempo, si la amplitud de cualquier componente es máxima, entonces la amplitud de otro componente se vuelve cero debido a la diferencia de fase.
También se describe como si la amplitud de cualquiera componente aumenta gradualmente, luego la amplitud de otro componente disminuye gradualmente y viceversa. Por lo tanto, la magnitud del vector resultante E ̅ es constante en cualquier instante de tiempo, pero la dirección es la función del ángulo entre las amplitudes relativas de E ̅y y E ̅x en cualquier momento.
Si la electricidad resultante el campo E ̅ se proyecta en un plano perpendicular a la dirección de propagación, luego el lugar geométrico de todos esos puntos es un círculo con el centro en el eje z como se muestra en la figura.
Durante el intervalo de una sola longitud de onda, el vector de campo E ̅ gira 360 grados o, en otras palabras, completa un ciclo de rotación y, por lo tanto, se dice que dichas ondas están circularmente polarizadas.
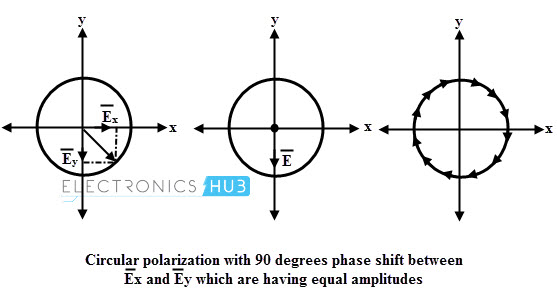
La polarización circular se genera como polarización circular derecha (RHCP) o polarización circular izquierda (LHCP). La onda RHCP describe una onda con el vector del campo eléctrico girando en el sentido de las agujas del reloj cuando se mira en la dirección de propagación.
Para una onda LHCP, el campo vectorial gira en sentido antihorario. Por lo tanto, la polarización de una onda plana uniforme es circular si las amplitudes de dos componentes del vector de campo eléctrico son iguales y tienen una diferencia de fase de 90 grados entre ellos.
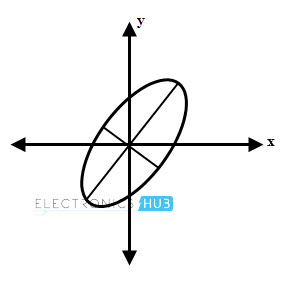
Polarización elíptica
En la mayoría de los casos, la los componentes de la onda tienen diferentes amplitudes y se encuentran en diferentes ángulos de fase que no sean 90 grados. Esto da como resultado la polarización elíptica. Considere que el campo eléctrico tiene ambos componentes E ̅x y E ̅y que no son iguales en amplitud y no están en fase.
A medida que la onda se propaga, los valores de amplitud máxima y mínima de E ̅x y E ̅y no simultáneos y están ocurriendo en diferentes instantes del tiempo. Por lo tanto, la dirección del vector de campo resultante varía con el tiempo.
Si se traza el lugar geométrico de los puntos finales del vector de campo E ̅ trazado, se puede observar que E ̅ se mueve elípticamente en el plano. Por lo tanto, dicha onda se denomina polarizada elípticamente.
Propagación de ondas EM en diferentes medios
In campos electromagnéticos, los materiales se clasifican como conductores, dieléctricos y dieléctrico con pérdidas. Los parámetros eléctricos como μ, є y σ son los parámetros variables que deciden el tipo de medio. Diferentes materiales afectan a los materiales de manera diferente.
Supongamos que si pasamos por un túnel o debajo del puente, nuestra radio deja de recibir las señales y, además, en comparación con el día, durante la noche, experimentaremos una mejor recepción de señales de radio. Por lo tanto, las olas se ven afectadas por los materiales o las condiciones ambientales.
Por lo tanto, es necesario conocer la propagación de las ondas electromagnéticas para elegir los valores apropiados de frecuencia, potencia, tipo de onda y otros parámetros necesarios para el diseño de las aplicaciones incluye líneas de transmisión, antenas, guías de onda, etc.
Considere las ondas obtenidas para un medio de las ecuaciones 5 y 6 como
∇2 E ̅ = μ σ × ∂ E ̅/∂t + μ є (E2 E ̅/∂t2)
∇2H ̅ = μ σ (∂ H ̅/∂t) + μ є (∂2H ̅ /∂t2)
Los campos eléctricos y magnéticos varían con el tiempo para una onda plana uniforme. Entonces, la derivada parcial con el tiempo respectivo puede ser reemplazada por jw. Por lo tanto, los campos eléctricos y magnéticos se pueden escribir como
∇2E ̅ = μ σ × (jw E ̅) + μ є (jw) 2 E ̅
∇2E ̅ = [jwμ (σ + jw є)] E ̅
Del mismo modo
∇2 H ̅ = [jwμ (σ + jw є)] H ̅
Las dos ecuaciones anteriores se llaman ecuación de onda en forma de onda En las ecuaciones anteriores, los términos dentro del paréntesis son los mismos y las propiedades del medio a través del cual se propaga la onda están representadas por este término. Este término es igual al cuadrado de una constante de propagación ɣ. Entonces las ecuaciones de onda se convierten en
∇2 E ̅ = ɣ2 E ̅
∇2 H ̅ = ɣ2 H ̅
En términos de las propiedades del medio, la constante de propagación se da como
ɣ = √ [jwμ ( σ + jw є)] = α + j β
En general, la onda se atenúa cuando viaja a través de un medio, por lo que la amplitud de la onda se atenúa. Esto está representado por la parte real de la constante de propagación y está dada por
α = w √ ((μ є/2) √ (1 + (σ)/w є) 2))-1)
De manera similar, el cambio de fase ocurre en una onda cuando se propaga a través de un medio. Este cambio de fase se representa como parte imaginaria de la constante de propagación y se da como
β = w √ ((μ є/2) √ (1 + (σ)/w є) 2)) + 1
Y también la impedancia intrínseca de un medio se puede expresar como
η = √ [( jwμ)/(σ + jw є)] Onda plana uniforme en espacio libre
Para espacio libre J = 0, σ = 0, є = єo y μ = μo, entonces las propiedades de la constante de propagación son
α = 0 y
β = w √ (μo єo)
Por lo tanto, la constante de propagación es puramente imaginaria para el espacio libre.
Onda plana uniforme en dieléctrico sin pérdida
Para un dieléctrico perfecto o sin pérdidas, las propiedades se dan como, σ = 0, є = єo єr y μ = μo μr. Tanto en el medio espacial libre como en el medio dieléctrico sin pérdidas σ = 0, el análisis de la propagación de la onda es muy similar en ambos casos. Pero como los valores de permeabilidad y permitividad son diferentes, la expresión en ambos casos varía.
La velocidad de propagación, v = (1/√ (μ є))
= (1/√ (μo μr єo єr)) = 1/(√ (μo єo) √ (μr єr))) = 1/(√ (μo єo)/√ (μr єr) ))
Por lo tanto, v = c/√ (μr єr) m/s
The constante de propagación,
ɣ = √ [jwμ (σ + jw є)] m-1
Sustituyendo σ = 0, є = єo єr y μ = μo μr en la ecuación anterior para un dieléctrico perfecto o sin pérdida, obtenemos
ɣ = +/-jw √ (μє) m-1
Y también constante de atenuación, α = 0
La constante de fase,
β = w √ (μ є) rad/m
Impedancia intrínseca,
η = √ [(jwμ)/(σ + jw є)] ohmios
= √ (μo/єo) √ (μr/єr)
= η o√ (μr/єr)
η = 377√ (μr/єr) ohms
Onda plana uniforme en dieléctrico con pérdida
Un dieléctrico con pérdida es un aislante pobre, en el que los cargos gratuitos conducen en cierta medida. Es un conductor imperfecto y dieléctrico imperfecto (que es un medio conductor parcial) con σ ≠ 0.
La constante de propagación se da como
ɣ = √ [jwμ (σ + jw є)]
Reordenando los términos, obtenemos
ɣ = √ [jw є (1 + (σ/jw є)) jwμ]
Por lo tanto, ɣ = α + j β = jw √μє √ (1-j (σ/w є))
La ecuación anterior proporciona la constante de propagación para un medio dieléctrico con pérdidas que es diferente del medio dieléctrico sin pérdidas debido a la presencia de un factor radical. La constante de atenuación α y la constante de fase se calculan sustituyendo los valores de w, μ, є y σ en la ecuación anterior.
La constante de atenuación α indica la pérdida cierta de la señal de onda en el medio y por lo tanto, este tipo de medio se denomina dieléctrico con pérdidas.
Y también debido a σ ≠ 0, la impedancia intrínseca se convierte en una cantidad compleja y se da como
η = √ [] (jwμ)/(σ + jw є)]
η = | η | ∠ Өn Ohms.
Debido a la cantidad compleja, η se representa en forma polar como se muestra en la ecuación anterior, donde Өn es la diferencia de ángulo de fase entre los campos eléctricos y magnéticos. Por lo tanto, en un medio dieléctrico con pérdidas, existe una diferencia de fase entre los campos eléctrico y magnético.
La impedancia intrínseca se puede expresar como
η = √ [(jwμ)/(σ + jw є)]
= √ [(jwμ)/jw є (1 + (σ/jw є)]
η = (√ (μ/є)) (1/√ (1-j (σ/w є)) ohmios
Y el ángulo Өn se da como
Өn = ½ [(π/2)-tan-1 (w є/σ)]
This el ángulo depende de la frecuencia de la señal así como de las propiedades del medio dieléctrico con pérdidas. Entonces, w se vuelve muy pequeño para una señal de baja frecuencia. Por lo tanto, el ángulo de fase se da como
Өn = (π/4)
Para señales de muy alta frecuencia, w llega a ser muy grande,
Өn = 0
Entonces el rango de Өn de un dieléctrico con pérdidas para un rango de frecuencia completo es 0 Өn (π/4).
Aplicaciones del Electroma ondas magnéticas
En general, un fenómeno de onda constituye tanto campos eléctricos como magnéticos variables en el tiempo. Algunas de las aplicaciones donde se pueden encontrar las ondas electromagnéticas se dan a continuación. Además de las áreas de aplicación a continuación hay muchas otras aplicaciones donde el conocimiento de las ondas electromagnéticas se utiliza profundamente.
Líneas de transmisión
En el caso de transmisión de potencia a bajas frecuencias, parámetros eléctricos como resistencia, capacitancia, inductancia, etc. son suficientes para caracterizar el circuito eléctrico completo. En dicho análisis de circuitos, no se considera el tamaño físico de los componentes eléctricos y las simples leyes de Kirchoff son suficientes para analizar el circuito.
Sin embargo, si se aumenta la frecuencia, se debe considerar el tamaño de los parámetros físicos y también el espacio comienza a desempeñar un papel en el análisis del circuito.
En dicha transmisión, los voltajes y las corrientes existen en forma de ondas. Este tipo de enfoque para analizar el circuito con inclusión de espacio se denomina enfoque de línea de transmisión.
Antenas
Una antena es uno de los dispositivos más importantes en el sistema de comunicación, aunque aparece como un dispositivo de aspecto pasivo. Puede lanzar y recibir ondas electromagnéticas de manera eficiente. Se han utilizado varios tipos de antenas para servir diferentes aplicaciones.
Con los avances en las comunicaciones móviles, se desarrollan antenas compactas, multifrecuencia y eficientes durante los últimos años. Al usar una potencia que varía desde unos pocos vatios a megavatios, la comunicación se establece mediante estas antenas.
Comunicaciones móviles
La comprensión del entorno de radio requiere el conocimiento de la propagación de ondas electromagnéticas. En un sistema celular, se emplean diferentes esquemas de reutilización de frecuencias dependiendo de la variación de la intensidad de la señal en función de la distancia. Uno de los principales aspectos importantes de la comunicación móvil se está desvaneciendo.
Por lo tanto, para predecir correctamente el comportamiento del desvanecimiento, los algoritmos de procesamiento de la señal necesitan el conocimiento del entorno de la radio. Por lo tanto, las ondas electromagnéticas y su análisis desempeñan un papel clave en los sistemas de comunicación móvil.
Comunicación de fibra óptica
Una comunicación de larga distancia eficiente y de alta velocidad utiliza una variedad de dispositivos de fibra óptica que se desarrollan empleando fenómenos complejos de electromagnética olas. Esta comunicación es la forma moderna de comunicación de onda guiada.
Para la investigación se usa la teoría de la propagación de la luz en las fibras ópticas electromagnéticas. Debido a la consecuencia directa de la consecuencia directa de la onda, la naturaleza de la luz produce una propagación modal dentro de una fibra óptica. También para analizar los detectores de fotos y láser, la teoría de ondas electromagnéticas es muy importante.
Interferencia electromagnética (EMI) y compatibilidad
En general, un circuito eléctrico tiende a dar radiación electromagnética, especialmente cuando están cambiando intensas corrientes. Esta radiación puede interferir con otras partes o elementos de la red, afectando así el rendimiento general del circuito.
El caso de ejemplo es SMPS y los circuitos digitales de alta velocidad producen una considerable interferencia electromagnética. La mayoría de los circuitos de protección se utilizan para proteger los circuitos de EMI. Por lo tanto, el diseño adecuado de tales escudos EMI requiere el conocimiento de las ondas electromagnéticas.
Radioastronomía
La radioastronomía es una combinación de ingeniería física y electrónica. Es una de las principales áreas importantes donde la comprensión de las ondas electromagnéticas es necesaria. En astronomía, las observaciones del cielo se llevan a cabo en frecuencias de radio.
Estas señales de RF son de naturaleza muy débil y, por lo tanto, se utilizan receptores de comunicación de arte y se usan antenas para detectar tales señales. Por lo tanto, en la radioastronomía se emplean todos los aspectos de las ondas electromagnéticas.