En general, los campos magnetostáticos se producen por el movimiento de cargas eléctricas con una velocidad uniforme, mientras que los campos electrostáticos se producen por las cargas estacionarias. Por otro lado, los campos electromagnéticos son los campos variables en el tiempo producidos por corrientes que varían en el tiempo.
Estos campos hacen que se genere fem basado en el principio de inducción electromagnética. En 1831, el físico inglés Michael Faraday y el científico estadounidense Joseph Henry descubrieron simultánea e independientemente que cualquier cambio en el campo magnético de una bobina de alambre provocaría una fem o voltaje en esa bobina.
El fenómeno de generación de fem del campo magnético se llama inducción electromagnética. Dos aplicaciones familiares de este principio son el generador eléctrico o alternador que es la fuente de energía eléctrica y el transformador que aumentan o disminuyen la fem de un circuito de CA.
Contenido
¿Qué es la inducción electromagnética? ?
El fenómeno o método de obtener una fem inducida en un conductor cortando las líneas de flujo por el conductor se llama inducción electromagnética. La fuerza electromotriz, fem no es fuerza como su nombre lo indica, pero es la trabajo por unidad de carga hecha por la fuerza.
Tiene las dimensiones de energía por carga. Esta fem se puede generar de dos maneras, que se obtienen a partir de los experimentos de Faraday, a saber, la bobina estacionaria, el imán móvil y el imán estacionario, la bobina móvil. Vamos a entender estos dos en breve.
Bobina estacionaria e imán móvil
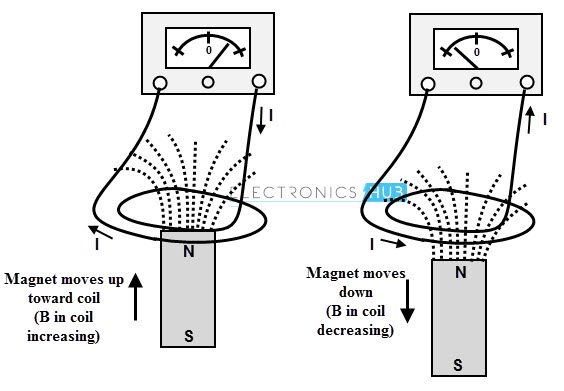
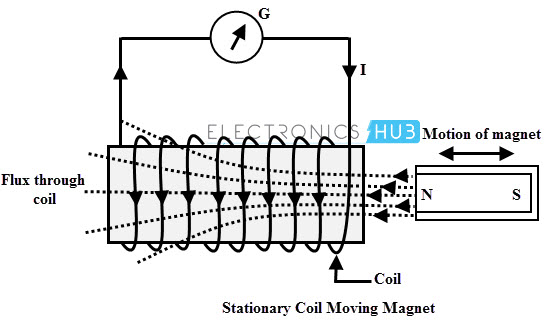
En este método, una bobina de N vueltas se mantiene constante y el imán permanente que produce las líneas magnéticas se mueve con relación a la bobina. Considere la siguiente figura en la cual una bobina que tiene N vueltas está conectada al galvanómetro que da la indicación de la corriente en el circuito.
Un imán permanente se mueve de tal manera que las líneas magnéticas a través de la bobina cambian. Entonces las estadísticas del galvanómetro se desvían cada vez que hay un movimiento de imán permanente. Más será la deflexión del galvanómetro cuando el imán permanente se mueva más rápido.
La razón de este flujo de corriente es la generación de fem por el movimiento de las líneas de flujo con respecto a la bobina estacionaria. Esta fem conduce el flujo de corriente a través del circuito.
Imán estacionario y bobina móvil
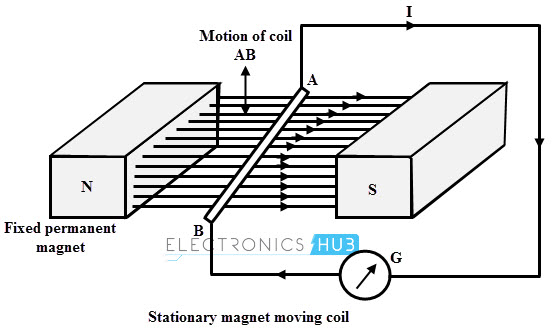
Esta es otra forma de obtener EMF moviendo una bobina en el campo magnético producido por el imán estacionario. La siguiente figura muestra una disposición que consiste en una bobina AB, que se mueve por medios externos y se conecta a un galvanómetro para indicar el flujo de corriente.
Cuando el conductor AB se mueve hacia arriba o hacia abajo, hay está cortando las líneas de flujo por el conductor. Por lo tanto, se induce una fem en el conductor y la corriente comienza a fluir a través del circuito, por lo que el galvanómetro comienza a desviarse.
La dirección del flujo de corriente está determinada por el movimiento del conductor en el campo magnético. Más será el flujo de corriente si el conductor se mueve rápidamente.
De los dos métodos anteriores, se debe notar que para tener fem inducida, debe haber un cambio en las líneas de flujo magnético con respecto al conductor. Los elementos necesarios para tener esta fem inducida son un conductor o bobina, un campo magnético (electroimán o imán permanente) y movimiento relativo entre el flujo magnético y el conductor.
Las leyes de Faraday de Inducción Electromagnética
Como se indicó anteriormente, dos científicos descubrieron la inducción electromagnética, a saber, Michael Faraday y Joseph Henry. Desde que Michael Faraday publicó su descubrimiento primero e investigó con más detalle sobre la inducción electromagnética, la ley que describe la inducción electromagnética lleva su nombre. Estableció dos leyes de inducción electromagnética.
Primera Ley de Faraday
Establece que cada vez que las líneas de fuerza magnética (flujo magnético) vinculadas con un circuito cerrado cambian o alternativamente cada vez que un conductor corta o es cortado por el flujo magnético, se induce una fem en el circuito que resulta en el flujo de corriente inducida a través del circuito. Mientras el flujo magnético cambie o el movimiento relativo persista entre el conductor y el flujo magnético, esta fem es inducida.
Segunda ley de Faraday
Establece que la magnitud de la fem inducida en un circuito o bobina es directamente proporcional a velocidad de cambio de los enlaces de flujo.
Considere una bobina que tiene N vueltas y el flujo inicial que se une como Φ1. Por lo tanto, los enlaces de flujo iniciales asociados con la bobina son N Φ1. Durante el tiempo t, el flujo que conecta con la bobina cambia de Φ1 a Φ2. Entonces el enlace de flujo final de la bobina es N Φ2.
Por lo tanto, la tasa de cambio de los enlaces de flujo = (N Φ2-N Φ1)/t
De acuerdo con Faraday ley, se generaría una fem en la bobina debido al cambio de los enlaces de flujo, y según la segunda ley, esta fem es proporcional a la tasa de cambio de los enlaces de flujo. es decir,
e α (N Φ2-N Φ1)/t
e = (N Φ2-N Φ1)/t
e = N dΦ/dt
Donde dΦ/dt es la tasa de cambio de flujo
N es el número de vueltas de la bobina
Esta fem inducida produce la corriente en una dirección tal que se opone a la misma causa de su producción de acuerdo con la ley de Lenz. Esta oposición se representa mediante un signo negativo matemáticamente como
e =-N dΦ/dt………………. (1)
La fem inducida es una cantidad escalar que se mide en voltios. Se puede escribir en términos de campo eléctrico como
e = ∮Ē. (DL̄)…………. (2)
La tensión de ecuación anterior sobre una trayectoria cerrada de modo que si se cambia cualquier parte de la ruta, la fem inducida cambiará.
El flujo magnético total que pasa a través de un área específica en términos de campo magnético se da como
Φ = ∮s B̄. (ds) ̄
WhereB es la densidad de flujo magnético
Luego se convierte en la ecuación 2 (suponiendo que N = 1, es decir, una sola espira)
e =-d/dt (∮sB̄. (ds) ̄)…………… (3)
∮E ̅. (dL) ̅ =-d/dt (∮sB̄. (ds) ̄)…………. (4)
Esto se denomina forma integral de la ley de Lenz.
Al considerar la ecuación 4 y aplicar el teorema de Stroke, obtenemos
∮s ∇ × Ē. (ds) ̄) =-d/dt (∮sB̄. (ds̄)
Si el circuito es estacionario, la derivada de tiempo se puede mover dentro de la integral y luego se convierte en una derivada parcial como
∮s ∇ × Ē. (ds) ̄) =-∮ (s) (∂/∂t (BM. (Ds) M))
Luego equiparando las integrales
∇ × EM = ∂/∂t BM
Esto se denomina forma diferencial de la ley de Faraday.
Lenz ’ s ley
Esta ley se nombra después del físico alemán Heinrich Lenz, que lo derivó. Esta ley establece que la dirección de la fem inducida producida por la inducción electromagnética siempre es tal que tiende a establecer una corriente que se opone a la causa que es responsable de producirla.
Aquí la causa es un cambio de flujo que es responsable de producir la fem. Por lo tanto, la fem inducida siempre se opone a la causa de producción y se representa mediante un signo negativo en la expresión matemática de fem.
e =-N dΦ/dt
Considere la siguiente figura en la que la bobina está conectada a un galvanómetro. Deje que un imán de barra se mueva hacia la bobina. Este movimiento del imán induce una fem en la bobina, generando la corriente. De acuerdo con la ley de Lenz, la dirección de la corriente inducida es tal que se opone al movimiento del imán como se muestra en la figura.
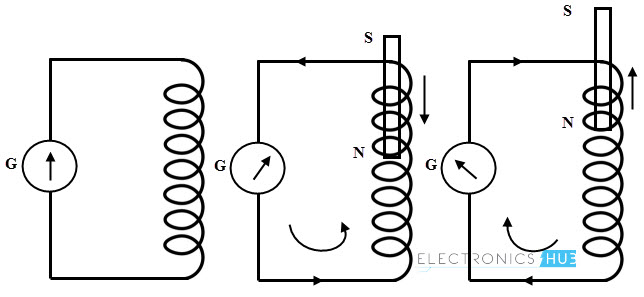
La corriente inducida debido a la fem genera su propio campo magnético que se opone al campo principal que causa la generación del emf. Entonces, el estado de Lenz de que la corriente inducida alrededor de un circuito cerrado es tal que un campo magnético producido por él trata de contrarrestar el cambio en el flujo magnético que causa la generación de fem.
En la figura siguiente, la corriente de lazo cerrado fluye en el sentido de las agujas del reloj debido a la fem inducida. De acuerdo con la ley de Lenz, si el campo magnético B aumenta, la corriente circulante genera un campo B ‘que se opone al aumento del flujo magnético B a través del bucle.
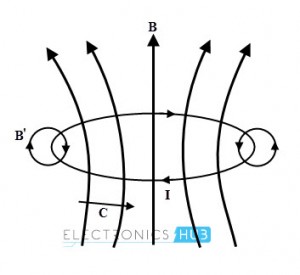
Luego la fem inducida en un ciclo cerrado se convierte en
∮C EM. (Dl) M) =-d/dt (∮sBM. (ds) M)
Donde el signo negativo representa la ley de Lenz
Inductancia
El efecto de inducción magnética en una bobina cuando dentro de los cambios del campo magnético con el tiempo está representado por la inductancia L. La causa para producir una fem en una bobina es la corriente que fluye a través de ella. Entonces, cualquier cambio en la corriente en una bobina se opone a la fem inducida de acuerdo con la ley de Lenz.
Esta propiedad de oponerse al cambio en la corriente se llama inductancia. Tal cambio de flujo dentro de la bobina tiene lugar no solo debido al cambio en la corriente en la bobina, sino también al cambio en las corrientes en las bobinas cercanas. Por lo tanto, la inductancia puede ser auto inductancia o inductancia mutua.
Auto Inductancia
Supongamos que un circuito dado es una bobina simple, luego cualquier cambio en la corriente cambia el flujo magnético asociado con la corriente. La propia bobina dada intercepta el flujo y el cambio en el flujo daría lugar a inducir la fem en la propia bobina. Esta fem se llama fem autoinducida, que impulsa la corriente inducida opuesta al cambio en la corriente.
Esto significa que cuando se aumenta la corriente, la fem inducida reduce la corriente y trata de mantener su valor original. De manera similar, si la corriente disminuye, la fem inducida aumenta la corriente e intenta mantener el valor original.
Por lo tanto, cualquier cambio en la corriente a través de la bobina se opone por la bobina y esta propiedad se denomina auto inductancia de la bobina. Dado que la fem inducida se opone a la causa de su producción, esta fem también se llama como fem o contra fem.
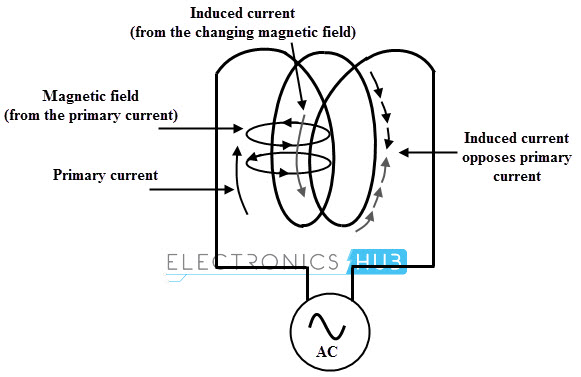
Si el circuito tiene N vueltas idénticas, entonces el enlace de flujo es igual a NΦ. Y también si el medio rodeado por el circuito es lineal, entonces el enlace de flujo es directamente proporcional a la corriente. es decir,
El enlace de flujo total, λ = NΦ y
λ α NΦ
λ α I
λ = LI
Donde L es la constante conocido como inductancia
L = λ/I
L = NΦ/I
Alternativamente
e =-N dΦ/dt
El flujo se puede expresar como
Φ = (Φ/I ) × I
Siempre que el medio sea lineal (la permeabilidad es constante), la relación entre el flujo y la corriente es constante.
Tasa de cambio de flujo = (Φ/I) × Tasa de cambio de corriente
dΦ/dt = (Φ/I) × dI/dt
Sustituyendo en la ecf fem, obtenemos
e =-N (Φ/I) × dI/dt
e =-(N Φ/I) × dI/dt
Donde (N Φ/I) es la auto inductancia y se denota como L. Se define como los enlaces de flujo por corriente de amperios y medidos en Henry (H ) Luego
e =-L dI/dt
Además, este coeficiente de auto inductancia se expresa como
L = NΦ/I
pero Φ = mmf/reluctancia
= NI/S
Entonces L = (N/I) × (NI/S)
L = (N2/S)
También Reluctane S = l/μa
Donde l es la longitud de la ruta de flujo magnético y a es el área de la sección transversal del circuito magnético a través del cual pasa el magnético.
Luego L = (N2/(l/μa))
L = (N2 μ a/l)
L = (N2 μo μr a)/l Henries
Inductancia mutua
El fenómeno de generar fem inducida en un el circuito al cambiar la corriente en otro circuito vecino se llama inducción mutua. Tenga en cuenta que dos bobinas que se colocan adyacentes entre sí como se muestra en la figura. La corriente a través de la bobina A produce el flujo Φ1 y parte de este flujo se vincula con la bobina B.
Esto se conoce como flujo mutuo Φ2. Si se cambia la corriente a través de la bobina A, entonces el flujo Φ1 también cambia. Como este flujo está asociado con la bobina B, el cambio del flujo mutuo Φ2 induce la fem en la bobina B. Esta fem se denomina fem mutua inducida.
Esta fem conduce la corriente a través de la bobina B. la inductancia mutua es la propiedad por la cual se induce fem en la bobina debido al cambio en la corriente en otra bobina.
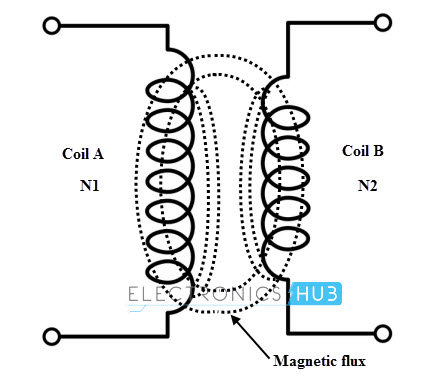
La fem inducida en la bobina B es
e2 =-N2 dΦ2/dt
El signo negativo representa que la fem inducida establece una corriente que se opone al cambio de flujo que se une con la bobina de acuerdo con la ley de Lenz.
Podemos expresar Φ2 = (Φ2/I1) × I1
Si la permeabilidad del medio es constante, Φ2 es proporcional a I1 y, por lo tanto, la relación (Φ2/I1) es constante. Tasa de cambio de Φ2 = (Φ2/I1) × Tasa de cambio de la corriente I1
dΦ2/dt = (Φ2/I1) × dI1/dt
Por lo tanto, la fem inducida es
e2 =-N2 (Φ2/I1) × dI1/dt
e2 =-(N2 Φ2/I1) × dI1/dt
En la ecuación anterior (N2 Φ2/I1) es la inductancia mutua y se denota como M. Se define como los enlaces de flujo total en una bobina por amperio cambio actual en otra bobina. Y se mide en Henries (H). Entonces, la fem inducida es
e2 =-M × dI1/dt
Además, esta inductancia mutua se expresa como
M = (N2 Φ2/I1)
Donde Φ2 es la parte del flujo Φ1 producida debido a I1. Considere que K1 es la fracción de Φ1 que está enlazando con la bobina B, es decir,
Φ2 = K1 Φ1
Then M = (N2 K1 Φ1/I1)
El flujo Φ1 se expresa como
Φ1 = mmf/Reluctancia
= (N1 I1)/S)
Por lo tanto, M = (N2 K1/I1) × (N1 I1)/S)
M = (K1 N1 N2)/S
Si el flujo total producido por la bobina A se vincula con la bobina B, entonces K1 = 1
M = (N1 N2)/S
Pero S = S = l/μa
Then M = ( N1 N2)/(l/μa)
M = (N1 N2 μo μr a)/l Henries
Esta es la inductancia mutua de la bobina B con respecto a la bobina A. Inductancia matemáticamente mutua de la bobina B debido a la bobina A y la inductancia mutua de la bobina A debida para bobina B es lo mismo.
Inductancia de un solenoide
Considere un solenoide que tenga N vueltas como se muestra en la figura. Y considere que la corriente que fluye a través del solenoide sea I amperios, A sea el área de la sección transversal y l sea la longitud del solenoide.
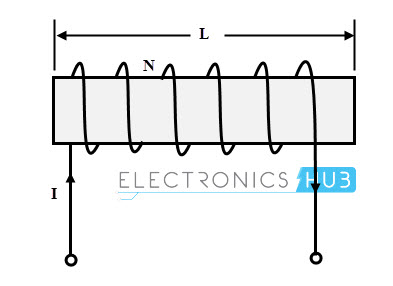
Se da la intensidad de campo del solenoide como
H = NI/l Ampere por metro
Total flux linkage = N Φ
= NBA
= N μH A
= μ NHA
Sustituyendo H en la ecuación anterior
Enlace de flujo total = μ N (NI/l) A
= (μ N2 IA)/l
Por lo tanto, la inductancia del solenoide se da como
L = Enlace de flujo total/corriente total
L = (μ N2 IA)/l)/I
L = μ N2 A)/l Henries
Inductancia de un Toroide
Considere un anillo toroidal de radio R con vueltas N se muestra en la figura a continuación. Deje que la corriente a través del anillo sea I amperio.
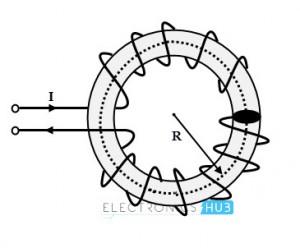
La densidad de flujo magnético dentro de un anillo toroidal se da como
B = (μ NI)/(2πR)
Los enlaces de flujo total en un anillo toroidal con N vueltas se dan como
Enlace de flujo total = N Φ </p>
= NBA (ya que Φ = BA)
= N ((μ NI)/(2πR)) A
= (μ N2 IA)/(2πR)
Por lo tanto, la inductancia e de un toroide es
L = Enlace de flujo total/Corriente total
= (μ N2 IA)/(2πR) (I)
L = (μ N2 A)/(2πR)
Wher A es la cruz área seccional del toroide que es igual a πr2 metros
Para un toroide con radio interno r1 y radio exterior r1, altura h con número total de vueltas N, la inductancia se da como
L = ((μ N2 h)/(2π)) ln (r2/r1)
Ejemplos de aplicación de inducción electromagnética
Generadores eléctricos
Un generador eléctrico produce la energía eléctrica de un trabajo mecánico (función opuesta del motor que convierte la energía mecánica en energía eléctrica).
El eje del generador eléctrico gira por algún medio mecánico como una turbina o un motor, con lo que se induce fem en los devanados de la bobina de acuerdo con las leyes de Faraday de inducción electromagnética.
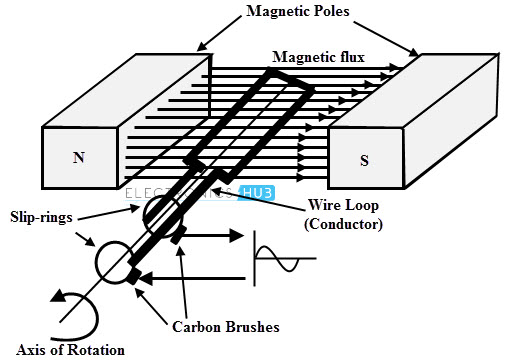
La operación principal del generador eléctrico se explica por una bobina de alambre que es rotado por un campo magnético uniforme como se muestra en la figura anterior. Pero en el generador práctico, el cable generalmente se enrolla en el núcleo de hierro.
Cada cable se forma como una bobina y los extremos de las bobinas se conectan al circuito externo por medio de anillos deslizantes que giran con la bobina.
El circuito externo está conectado a las escobillas estacionarias que entran en contacto con los anillos deslizantes cuando cada anillo se desliza. En los generadores, el flujo magnético puede ser móvil o estacionario depende del conductor estacionario o en movimiento.
En la figura anterior, el flujo estacionario es producido por los imanes permanentes y el conductor o bobina se mueve con respecto a el flujo estacionario. Debido al movimiento relativo entre el conductor y el flujo, se inducirá una fem en la bobina o el conductor.
Esta fem conduce la corriente al circuito de carga externo. Cuando el plano del movimiento del conductor es paralelo al plano del flujo, la fem inducida es cero y cuando es perpendicular, la fem inducida será máxima. Esta fem también recibe el nombre de fem inducida dinámicamente.
Transformador
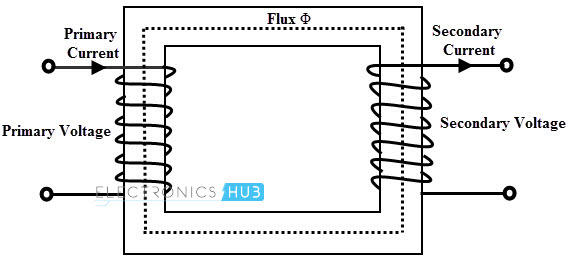
Un transformador consiste esencialmente en dos o más devanados en un núcleo de hierro cerrado. Al usar el transformador, la potencia puede transformarse de un circuito de corriente alterna a otro con el cambio deseado en los niveles de voltaje y corriente. El transformador funciona según el principio de inducción mutua entre dos bobinas.
Cuando se aplica una tensión al arrollamiento primario, una corriente pasa a través de él y configura un flujo magnético en el núcleo. Este flujo induce una fem en la bobina primaria que debe ser exactamente igual y opuesta a la tensión aplicada. El mismo flujo también está relacionado con el bobinado secundario en la otra extremidad del núcleo.
Así, el principio de inducción electromagnética induce una fem en el bobinado secundario. Las fem asociadas a los bobinados respectivos dependen del número de vueltas en cada bobinado. Por lo tanto, sin un acoplamiento eléctrico entre los circuitos, un transformador transfiere la energía de un circuito.
La relación de voltaje deseada de primario a secundario se obtiene seleccionando adecuadamente la relación de espiras de secundario a primario.
Además de estos ejemplos principales, existen numerosas aplicaciones que utilizan el principio de inducción electromagnética para su funcionamiento, como la transmisión de energía eléctrica, cocinas de inducción, hornos industriales, equipos médicos, sensores de flujo electromagnético, instrumentos musicales (como el violín eléctrico y la guitarra eléctrica) y s o encendido.