Los osciladores LC son ampliamente utilizados para generar ondas de alta frecuencia, por lo tanto, estos también se llaman osciladores de RF. Es posible producir las frecuencias en un rango más alto (más de 500 MHz) con los valores prácticos de inductores y condensadores.
Estos tipos de osciladores se usan en generadores de RF, calefacción de alta frecuencia, receptores de radio y televisión, etc. Estos osciladores usan un circuito de tanque que consiste en elementos del inductor L y del condensador C. Antes de hablar sobre el circuito del oscilador LC y su funcionamiento, hablemos sobre el funcionamiento básico del circuito del tanque LC.
Circuito de tanque LC
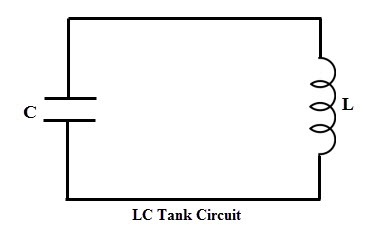
Un tanque o circuito oscilatorio es una forma paralela de elementos de inductor y condensador que produce las oscilaciones eléctricas de cualquier frecuencia deseada. Ambos elementos son capaces de almacenar energía. Cada vez que existe una diferencia de potencial en las placas de un condensador, almacena energía en su campo eléctrico.
De manera similar, cuando la corriente fluye a través de un inductor, la energía se almacena en su campo magnético. La figura a continuación muestra un circuito de tanque en el que el inductor L y el condensador C están conectados en paralelo.

Funcionamiento del circuito LC Tank
Permítanos entender el concepto de oscilaciones eléctricas producidas por este circuito. Tenga en cuenta que el condensador se carga inicialmente con una fuente de CC que tiene las polaridades placa superior positiva y placa inferior negativa como se muestra a continuación.
Esto representa que la placa superior tiene deficiencia de electrones, mientras que la placa inferior tiene exceso de electrones. Por lo tanto, existen posibles diferencias entre estas dos placas.

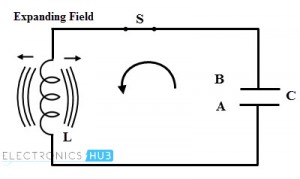
- Tenga en cuenta que este condensador cargado se conecta a través del inductor a través de un interruptor S como se muestra en la figura. Cuando el interruptor S está cerrado, el flujo de corriente convencional o los electrones se mueven de la placa A a la B a través de la bobina del inductor. Por lo tanto, la energía almacenada o la fuerza del campo eléctrico en el condensador disminuye.

- La corriente que fluye a través del inductor induce una EMF que se opone a los electrones fluyen a través de él. Este flujo de corriente configura un campo magnético alrededor del inductor, por lo que comienza a almacenar la energía magnética. Cuando el condensador está completamente descargado, el flujo de corriente o de electrones a través de la bobina se vuelve cero. En este momento, el campo magnético tiene el valor máximo y no hay campo eléctrico.

- Una vez que el condensador está completamente descargado, el campo magnético alrededor del inductor comienza a colapsar y produce el contador de fem. Según la ley de Lenz, esta contra fem produce la corriente que comienza a cargar el condensador con polaridad opuesta haciendo que la placa superior de la placa sea negativa y la placa inferior positiva, como se muestra en la figura a continuación.

- Cuando el condensador está completamente cargado en la dirección opuesta, toda la energía magnética se convierte de nuevo en energía eléctrica en el condensador, es decir, la energía magnética se colapsa. En este instante, el condensador comienza a descargarse en la dirección opuesta, como se muestra en la figura. Una vez más, el condensador está completamente descargado y este proceso continuará.
- Esto continuo el proceso de carga y descarga da como resultado un movimiento alterno de electrones que no es más que una corriente oscilante. Pero estas oscilaciones del condensador se amortiguan porque cada vez que se transfiere energía de L a C y C a L se disipa energía en forma de calor en la resistencia de la bobina y en los alambres de conexión en forma de radiación electromagnética. Estas pérdidas disminuyen gradualmente la amplitud de la corriente oscilante hasta que cesa. Estos se denominan oscilaciones exponencialmente decrecientes u oscilaciones amortiguadas.

Frecuencia del oscilador LC
Concepto de resonancia
Si el circuito con condensador, inductor y resistencia se excita con voltaje constante con frecuencia variable en el tiempo, entonces la reactancia del inductor-resistencia RL y del condensador-resistencia RC también son variados. Por lo tanto, la amplitud y la frecuencia de la salida varían en comparación con la señal de entrada.
La reactancia inductiva es directamente proporcional a la frecuencia, mientras que la reactancia capacitiva es inversamente proporcional a la frecuencia. Por lo tanto, en frecuencias más bajas, la reactancia capacitiva del inductor es muy baja y actúa como un cortocircuito, mientras que la reactancia capacitiva es alta y actúa como circuito abierto.
A frecuencias más altas, ocurrirá el reverso, es decir, actos de reactancia capacitiva como cortocircuito, mientras que la reactancia inductiva actúa como circuito abierto.
En una combinación particular de condensador e inductor, este circuito se convierte en circuito resonante o sintonizado que tiene una frecuencia resonante en la cual la reactancia inductiva y las reactancias capacitivas son idénticas y cancelar entre sí.
Por lo tanto, solo habrá resistencia en el circuito para oponerse al flujo de corriente y, por lo tanto, no habrá corriente de cambio de fase a partir de la tensión mediante el uso de un circuito resonante. La corriente está en fase con la tensión.
Las oscilaciones sostenidas se pueden obtener proporcionando la energía de suministro a los componentes L y C. Por lo tanto, los osciladores LC usan este circuito tanque para producir las oscilaciones.
La frecuencia de las oscilaciones generadas por este circuito tanque depende completamente de los valores de capacitor e inductor y su condición de resonancia. Se puede expresar como
XL = 2π f L
XC = 1/(2π f C)
En resonancia, XL = XC
2π f L = 1/(2π f C)
f2 = 1/((2π) 2 LC)
f = 1/(2π √ ( LC))
Forma Básica del Circuito del Oscilador LC
En este oscilador, el amplificador y la red de filtro LC se pueden construir de varias maneras. Por lo tanto, estos osciladores vienen en diferentes formas tales como osciladores Hartley, oscilador Armstrong, osciladores Colpitts, osciladores Clapp, etc. Antes de discutir sobre todos estos osciladores en otros artículos, aprendamos algunos aspectos básicos del circuito oscilador LC.
Como se mencionó anteriormente, un oscilador LC consiste en un amplificador y un circuito LC sintonizado como red de retroalimentación. Para el circuito del oscilador LC, la etapa del amplificador se puede construir mediante el uso de dispositivos activos como amplificador operacional, transistor de unión bipolar o FET.
La forma básica del oscilador se muestra a continuación con la ganancia A del amplificador. la red consta de impedancias Z1, Z2 y Z3 que pueden ser de capacitancia o inductancia. Esta red de retroalimentación se suministra con la salida del amplificador.

El circuito amplificador proporciona un desplazamiento de fase de 180 grados mientras que el circuito de retroalimentación proporciona un desplazamiento de fase adicional de 180 grados para satisfacer la condición de oscilaciones Considere el circuito equivalente del oscilador LC en el que Ro es la resistencia de salida del amplificador y ZL es la impedancia de carga conectada a la salida del amplificador.

La expresión de ganancia general del amplificador para el circuito anterior con carga (AL) y sin considerar la realimentación está dado por
AL =-A ZL/(Ro + ZL)
El signo negativo indica el desplazamiento de 180 fases en la etapa del amplificador.
Al considerar la retroalimentación, la ganancia de la red de retroalimentación viene dada por
β = Z1/(Z1 + Z3)
Pero esta red de retroalimentación debe introducir 180 digress shift shift y luego
β =-Z1/(Z1 + Z3)
Para satisfacer la condición de oscilaciones de Barkhausen,-Aβ debe ser igual a 1, luego
A β =-A ZL Z1/(Ro + ZL) × (Z1 + Z3)
Esta es la expresión de ganancia de bucle requerida.
Ahora, la impedancia de carga ZL = Z2 (Z1 + Z3)/(Z1 + Z2 + Z3)
Resolviendo la expresión de ganancia del bucle con ZL, entonces obtenemos
A β =-A Z1 Z2/(Ro (Z1 + Z2 + Z3) + Z2 (Z1 + Z3))
Sustituyendo Z1 = j X1, Z2 = j X2 y Z3 = j X3
A β = A X1 X2/(jRo (X1 + X2 + X3)-X2 (X1 + X3))
Para producir el desplazamiento de 180 fases por esta red de retroalimentación, la parte imaginaria del denominador debe ser cero, es decir,
(X1 + X2 + X3) = 0 esto implica que-X2 = X1 + X3
Entonces la ecuación se convierte en
A β = A X1/(X1 + X3)
A β =-A (X1/X2)
Pero la condición de Barkhausen es-Aβ = 1. Entonces
A (X1/X2) = 1
Esto significa que X1 y X2 deben ser inductivos o capacitivos (tipo similar de reactancia) y la condición para oscilaciones se obtiene como
A = (X2/X1)
Para el oscilador Hartley, tanto X2 como X1 son inductores, mientras que para los osciladores Colpitts ambos son condensadores. Y también-X3 = X1 + X2, así X3 es un condensador en el oscilador Hartley y es un inductor en el oscilador Colpitts.
Ejemplo
Averigüe el valor del inductor necesario con un condensador de 47 pF para un oscilador LC sintonizado frecuencia de 22.7 MHz. La frecuencia de resonancia del oscilador LC es
f2 = 1/((2π √ (LC)) 2
L = 1/(4π2 f2 C)
L = 1/(4π2 (22.7 × 106) 2 × 47 × 10-12) L = 1.04micro Henry