Contenido
Definición de diferencia de potencial
Considere la tarea de mover una carga de A a B en un campo eléctrico uniforme. Deje que este movimiento sea contrario al campo eléctrico. Algún trabajo será hecho por una fuerza externa en esta carga y este trabajo cambiará la energía potencial a un valor más alto. La cantidad de trabajo realizado es igual al cambio en la energía potencial. Este cambio en la energía potencial dará como resultado una diferencia en el potencial entre los dos puntos A y B. Esta diferencia de potencial se llama diferencia de potencial y se mide en voltios (V).
La diferencia de potencial se denota por ΔV y se define como la diferencia en potencial o voltaje entre dos puntos. Si VA es el potencial en A y VB es el potencial en B, entonces a partir de la definición de diferencia de potencial,
ΔVBA = VB-VA
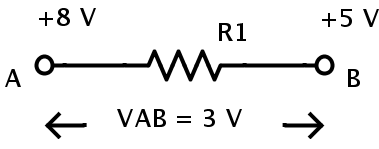
Por ejemplo, considere la siguiente resistencia R1.
| | []
El potencial aplicado en un extremo de la resistencia (Punto A) es de 8 V y el potencial en el otro extremo de la resistencia (Punto B) es de 5 V.
La diferencia de potencial entre los dos puntos A y B es
VAB = 8-5 = 3 V.
Esto también se denomina Potencial a través de la resistencia.
La corriente fluye en un circuito eléctrico en forma de carga, mientras que el potencial no fluye ni se mueve. La diferencia potencial se aplica entre dos puntos.
La unidad de diferencia de potencial entre dos puntos es Volt. Volt se define como la caída de potencial a través de una resistencia de 1 ohmio (Ω) con 1 amperio de corriente que fluye a través de ella.
Por lo tanto,
1 Volt = 1 Amperio × 1 Ohm
V = I × R
Según la ley de Ohm, la corriente que fluye en un circuito lineal está directamente proporcional a la diferencia de potencial en todo el circuito. Por lo tanto, si la diferencia de potencial aplicada a través del circuito es mayor, entonces la corriente que fluye en el circuito es mayor.
Por ejemplo, si un lado de un resistor de 1 Ω está a un potencial de 8 V y el otro lado está a 2 V, entonces la diferencia de potencial entre la resistencia es 5 V. La corriente que fluye en la resistencia es
I = V/R = 5V/1 Ω = 5 Amps.
Ahora para la misma resistencia de 1 Ω, si el potencial aplicado en un extremo se eleva de 8 V a 12 V y en el otro extremo se eleva de 2 V a 4 V. Luego la diferencia de potencial entre la resistencia es ahora de 8 V. La corriente que fluye en la resistencia en esta situación es de 8 amperios.
I = V/R = 8V/1 Ω = 8 Amps.
Generalmente en circuitos eléctricos, el potencial más bajo es tierra o tierra. Este valor generalmente se considera 0 V. Por lo tanto, la diferencia de potencial es igual al voltaje aplicado. La Tierra se considera como el punto común en un circuito. Esta referencia de tierra o tierra como punto común en los circuitos eléctricos es útil para una fácil comprensión del circuito. La diferencia de potencial también se llama voltaje.
Las tensiones conectadas en serie se agregan para dar voltaje total en un circuito. Esto se puede observar en resistencias en conexión en serie. Si V1, V2 y V3 están conectados en serie, el voltaje total VT viene dado por
VT = V1 + V2 + V3.
In caso de elementos conectados en paralelo, el voltaje a través de ellos es igual. Esto se puede observar en resistencias en paralelo tutorial.
VT = V1 = V2 = V3.
Ejemplos de diferencias de potencial
- Si se transfieren 1500 Joules de energía potencial para mover una carga de 125 Coulomb entre los terminales de una batería, la diferencia de potencial es
ΔE = 1500 J
Q = 125 C
Diferencia de potencial V = ΔE/C
V = 1500/125 = 12 Joules/Coulomb = 12 V
2. Considere una resistencia de resistencia de 10 Ω. Deje que un extremo de la resistencia se conecte a un potencial de 15 V. Deje que el otro extremo de la resistencia se conecte a un potencial de 5 V. La corriente que fluye a través de la resistencia se puede calcular de la siguiente manera.
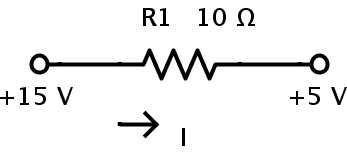
Los dos terminales de la resistencia tienen dos potenciales diferentes, es decir, 15 V y 5 V, respectivamente. Deje que los dos terminales sean A y B. Por lo tanto, la tensión en A es VA = 15 V y la tensión en B es VB = 5 V. Entonces, la diferencia de potencial entre A y B es la tensión a través de la resistencia.
VAB = VA-VB = 15-5 = 10 V.
Entonces la corriente que fluye a través de la resistencia puede calcularse usando la ley de Ohm como
I = VAB/R = 10/10 = 1 amperios.
Circuito divisor de voltaje
Las resistencias en conexión en serie se utilizan para producir un circuito divisor de voltaje El divisor de voltaje es un circuito lineal cuya tensión de salida es una fracción del voltaje de entrada.
A continuación se muestra un circuito divisor de voltaje simple con 2 resistencias.
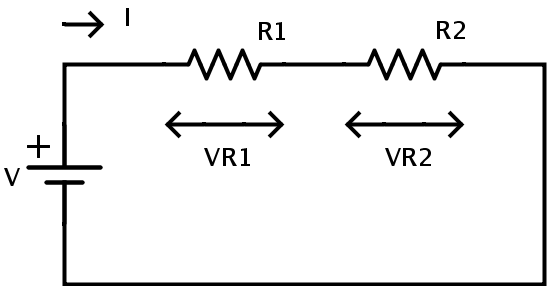
El potencial en cada resistencia en conexión en serie depende del valor de la resistencia. El principio del divisor de voltaje es producir un voltaje que es una fracción del voltaje de entrada.
El siguiente circuito se usa para mostrar el principio del divisor de voltaje para voltajes de salida múltiples.
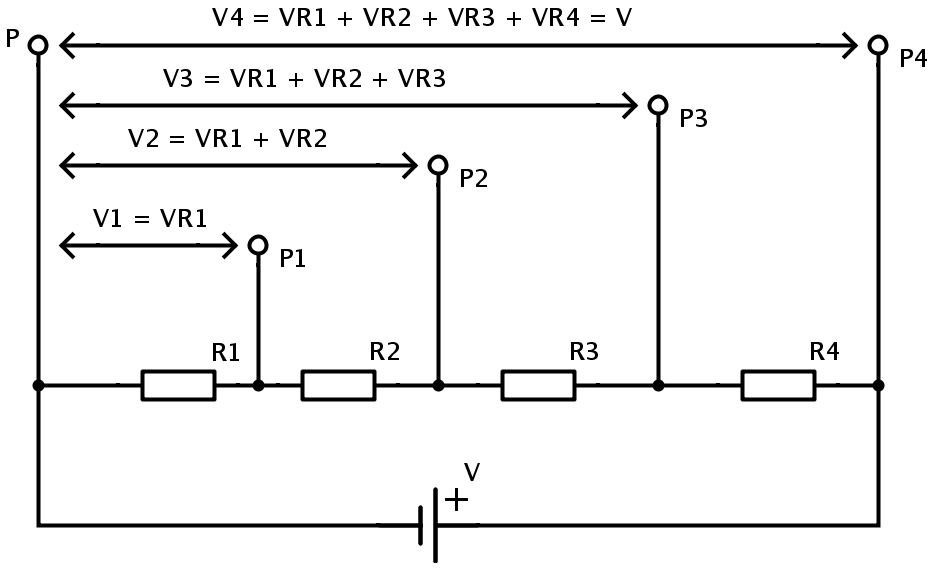
Aquí las resistencias R1, R2, R3 y R4 están en conexión de serie. La tensión de salida en cada resistencia está referenciada a un punto común P. Deje que la resistencia equivalente de las resistencias en serie sea RT. Luego RT = R1 + R2 + R3 + R4.
Deje que la diferencia de potencial en cada resistencia sea VR1, VR2, VR3 y VR4 respectivamente para R1, R2, R3 y R4. Entonces el circuito anterior puede producir 4 voltajes diferentes que son fracciones de la tensión de alimentación V.
Fórmula del divisor de tensión
El valor de la tensión de salida en un circuito divisor de tensión típico se calcula como sigue.
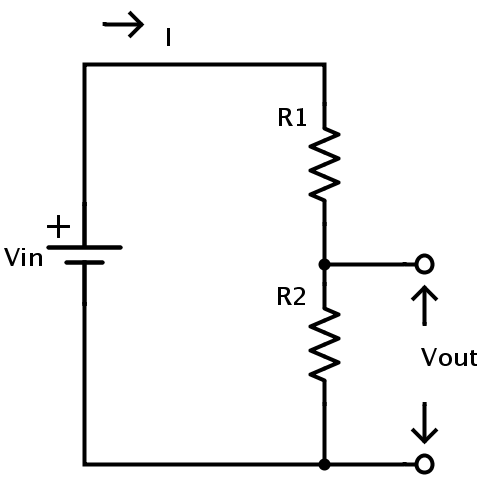
Aquí Vin es la tensión de alimentación. I es la corriente en el circuito que fluye a través de ambas resistencias.
Sea VR1 la caída de tensión a través de la resistencia R1 y VR2 la caída de tensión a través de la resistencia R2. Entonces la suma de estas caídas de voltaje individuales es igual a la tensión total a través del circuito que es la tensión de suministro Vin.
Vin = VR1 + VR2—1
Las ecuaciones para las caídas de voltaje individuales a través de cada resistencia se pueden calcular a partir de la ley de Ohm.
VR1 = I × R1—2
Y VR2 = I × R2—3
Pero el voltaje en la resistencia R2 es VOUT.
Por lo tanto VOUT = I × R2—4
Por lo tanto, a partir de las ecuaciones 1, 2 y 3
Vin = I × R1 + I × R2 = I × (R1 + R2)—5
Pero el valor de la corriente I en términos de voltaje de salida se puede escribir de la siguiente manera usando la ecuación 4.
I = VOUT/R2—6
Uso de las ecuaciones 5 y 6
VOUT = Vin × (R¬2/R1 + R2)
Por lo tanto, VOUT = VIN × R2/(R1 + R2)
En el caso del circuito divisor de voltaje que tiene salidas múltiples, los voltajes de salida se pueden calcular utilizando el siguiente fórmula.

VX = V × (RX/REQ)
Donde VX es la tensión que se va a encontrar.
RX es la resistencia total a través de la tensión de salida.
Los posibles valores de RX son
R1 entre P y P1
R1 + R2 entre P y P2
R1 + R2 + R3 entre P y P3
R1 + R2 + R3 + R 4 entre P y P4.
REQ es la resistencia equivalente de la resistencia en conexión en serie.
REQ = R1 + R2 + R3 + R4
V es la tensión de alimentación.
Por lo tanto, los posibles voltajes de salida son
V1 = V × R1/REQ
V2 = V × (R1 + R2)/REQ
V3 = V × (R1 + R2 + R3)/REQ
V4 = V × (R1 + R2 + R3 + R4)/REQ = V
Divisor de voltaje Ejemplo
Considere el siguiente circuito divisor de voltaje.
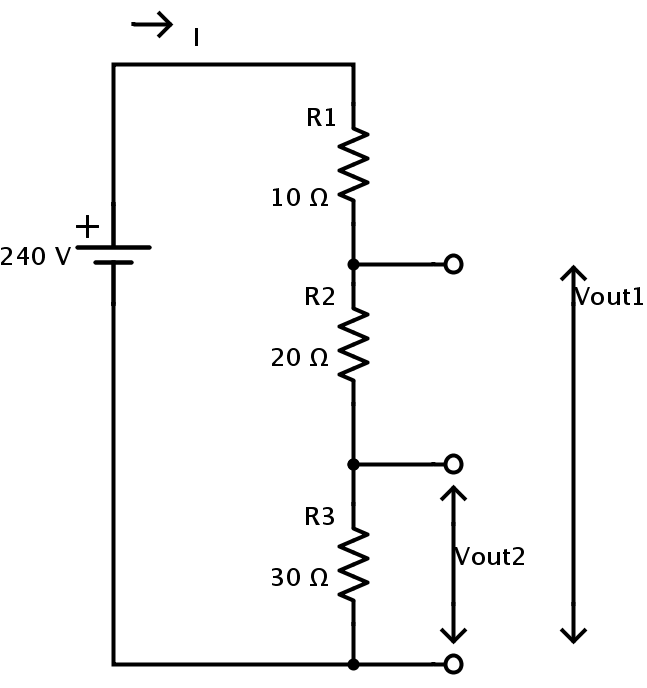
Consiste en tres resistencias conectadas en serie para producir dos voltajes de salida. La tensión de alimentación es 240 V.
Los valores de la resistencia son R1 = 10 Ω, R2 = 20 Ω y R3 = 30 Ω.
Por lo tanto, la resistencia equivalente del circuito es
REQ = R1 + R2 + R3 = 10 + 20 + 30 = 60 Ω.
Ahora se pueden calcular los dos posibles voltajes de salida de la siguiente manera
Vout1 = V × (R2 + R3)/REQ
Vout1 = 240 × (20 + 30)/60
Vout1 = 200 V.
Vout2 = V × R3/REQ
Vout2 = 240 × 30/60
Vout2 = 120 V.
La corriente en el circuito es
I = V/REQ = 240/60 = 4 amperios.
Por lo tanto, las caídas de tensión individuales en cada resistencia se pueden calcular de la siguiente manera
VR1 = I × R1 = 4 × 10 = 40 V.
VR2 = I × R2 = 4 × 20 = 80 V.
VR3 = I × R3 = 4 × 30 = 120 V.
Aplicaciones de Circuitos Divisores de Tensión
Las resistencias en serie formarán Circuitos Divisores de Tensión. El principio del divisor de voltaje es la base en la construcción del potenciómetro que actúa como un simple regulador de voltaje.
Los circuitos del divisor de voltaje se utilizan en los circuitos de detección. Los sensores utilizados con más frecuencia en forma de circuitos de divisor de voltaje son los termistores y las resistencias dependientes de la luz.