Cuando se aplican valores iguales de voltaje directo y voltaje alterno al mismo circuito que tiene un inductor en serie con la carga, fluiría más corriente en un circuito de CC que en un circuito de CA.
Esto se debe a que solo el voltaje inducido se opone al flujo de corriente en el circuito de CC cuando la corriente se aproxima a su valor máximo y una vez que alcanza un valor de estado estable, no habrá más efecto inductivo.
En el caso de los circuitos de CA, la corriente cambia continuamente, por lo tanto, el efecto inductivo está presente en todo momento. Considere los siguientes circuitos de CC y CA para comprender este concepto.
Contenido
Circuito inductivo de CC
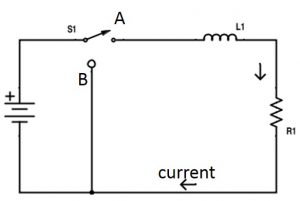
En la figura anterior, si el interruptor está en funcionamiento del nodo A al nodo B e inmediatamente del nodo B al nodo A, un cambio en los flujos de corriente t a través del circuito.
Este cambio en la corriente induce una fem en el inductor proporcional a la velocidad de cambio de la corriente y esta fem se opone a la tensión aplicada (que es la causa de la producción de corriente). Esto se llama autoinducción.
Una vez que la corriente alcanza un valor estable, no habrá autoinducción en el inductor y, por lo tanto, no habrá oposición al flujo de corriente.
Circuito inductivo de CA
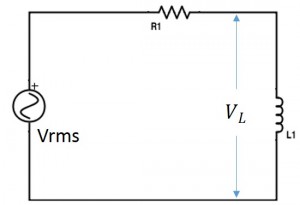
Sabemos que, cuando se aplica corriente de CA al circuito, la corriente cambia continuamente a una frecuencia de frecuencia de suministro y, por lo tanto, la fem de vuelta cambiará en consecuencia.
Esta fuerza de espalda se opone a la tensión de alimentación y, por lo tanto, el flujo de corriente es limitado. Por lo tanto, la oposición real al flujo de corriente creado por un inductor en un circuito de CA se conoce como la reactancia inductiva.
Reactancia inductiva en un inductor
En un circuito inductivo observando el autoinductancia y su efecto dentro del circuito, podemos definir la reactancia inductiva. El campo magnético induce el voltaje en el inductor que siempre es opuesto en polaridad al voltaje que lo produce, es decir, voltaje aplicado.
Este voltaje opuesto limita la corriente que fluye a través de un inductor y se llama reactancia ( X). Como esta reactancia es causada por la inductancia, se llama reactancia inductiva (XL). Se mide en ohmios.
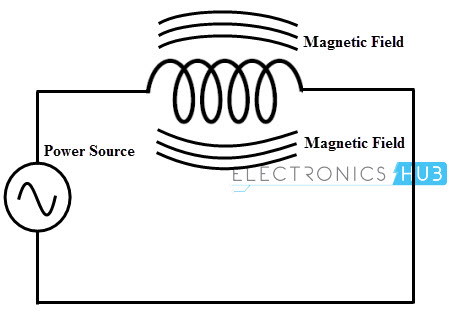
La cantidad de reactancia inductiva ofrecida por un inductor es proporcional a la inductancia y frecuencia del voltaje aplicado. Esta reactancia puede determinarse mediante la siguiente fórmula.
XL = 2 π fL
Donde XL = reactancia inductiva en ohmios
π = 3.14
f = frecuencia en hercios (Hz) )
L = inductancia en Henrys (H)
De acuerdo con la ley de ohmios, la reactancia inductiva es directamente proporcional al voltaje aplicado e inversamente proporcional a la corriente. Se puede expresar como
I = V/XL
De la ecuación anterior, está claro que el aumento de voltaje o la disminución de la reactancia inductiva causa una aumento en la corriente. Asimismo, la corriente disminuye con el aumento de la reactancia inductiva y la disminución de la tensión.
Cualquier inductor práctico debe fabricarse con alambre enrollado que consista en cierta resistencia, por lo que no es posible obtener una bobina puramente inductiva.
Por lo tanto, hay dos factores que se oponen al flujo de corriente en un inductor, a saber, la resistencia asociada con la bobina (que se considera como resistencia separada R en serie con el inductor) y la reactancia inductiva ofrecida por la propiedad de inductancia.
Por lo tanto, la propiedad de limitación de corriente total de un inductor en el circuito de CA es la combinación de resistencia y reactancia que se denomina impedancia, Z.
Este valor de impedancia se calcula mediante la ley de Ohm y se da como
Z = V/I
Donde Z = oposición total ofrecida por el inductor al flujo de corriente, en ohmios
V = voltaje aplicado
I = corriente que fluye a través de th e circuit
Impedance Triangle
Otro método para determinar la impedancia es el uso del método de triángulo de impedancia cuando se conocen los valores de reactancia inductiva y resistencia. El siguiente diagrama muestra un triángulo de impedancia que consiste en vectores de resistencia y reactancia.
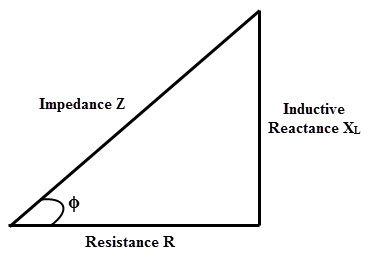
En la figura anterior, el vector de resistencia está junto con la línea horizontal (porque la resistencia no ofrece ningún cambio de fase) y el vector de reactancia inductiva está junto con la línea vertical (porque la inductancia pura ofrece 900 desplazamiento de fase).
Al conectar los extremos de estos dos vectores, se obtiene la impedancia, Z. Por lo tanto, la oposición total a la corriente o la impedancia se puede calcular mediante
Z = √ [(R) 2+ (XL) 2]
Donde
Z = impedancia en ohmios
R = resistencia en ohmios
XL = reactancia inductiva en ohmios
Además, en el diagrama anterior,
tan∅ = XL/R
sin∅ = XL/R
cos∅ = R/Z
Efecto de la frecuencia o la inductancia en la reactancia inductiva
Como se discutió anteriormente, la reactancia inductiva está determinada por la fórmula,
XL = 2 π f L
En la ecuación dada, el valor de la reactancia inductiva es proporcional a la inductancia y frecuencia.
La reactancia inductiva aumenta con el aumento de la inductancia o el aumento de la frecuencia. Por lo tanto, la reactancia inductiva varía linealmente con la inductancia y la frecuencia.
Así que la oposición al flujo de corriente aumenta con el aumento de la inductancia o frecuencia. Considere las siguientes tramas para una comprensión clara de esta relación.
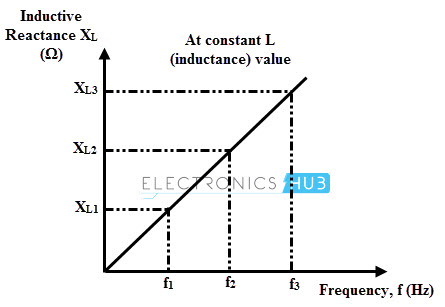
Considere la figura anterior, que representa la reactancia inductiva frente a la frecuencia a una inductancia fija. En la frecuencia cero, la reactancia inductiva es cero y, a medida que la frecuencia aumenta, la reactancia inductiva avanza adecuadamente.
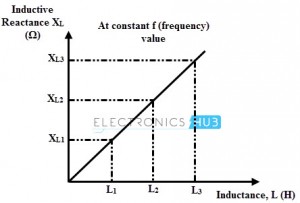
Considere la figura anterior que traza la reactancia inductiva frente a la inductancia a una frecuencia fija. Puede ser que a medida que aumenta la inductancia de un inductor, la reactancia inductiva también aumenta.
Ejemplo de reactancia inductiva
Consideremos un inductor con inductor de (L) 100uH a frecuencia de operación (f) 1 MHz. Luego, la inductancia inductiva se calcula de la siguiente manera:
XL = 2πfL = 2π × 1MHz × 100μH
XL = 628 Ω
Circuitos RL y reactancia inductiva
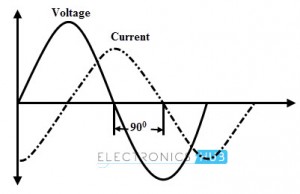
La figura siguiente muestra la relación entre la tensión aplicada y la corriente a través de un circuito inductivo. En un circuito inductivo puro, la corriente rezaga la tensión de la fuente en 900. También se puede establecer que el voltaje de la fuente conduce la corriente en 900 en un circuito inductivo.
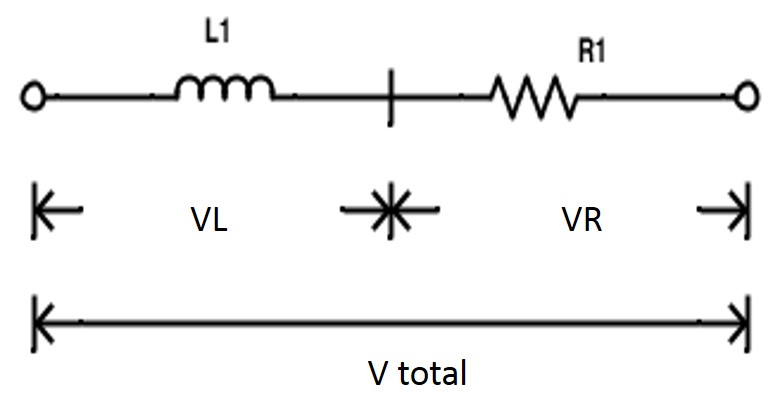
Cuando un inductor se conecta en serie con la resistencia RL, el circuito en serie se obtiene como se muestra a continuación. Esto también se puede considerar como inductancia que consiste en cierta resistencia (que se considera como resistencia en serie), como lo hizo a partir de un cable.
Por lo tanto, la corriente y la tensión no mantienen exactamente el cambio de fase 900, pero menos que el caso puramente inductivo como se muestra a continuación.

La figura siguiente muestra el diagrama vectorial del circuito serie RL que consiste en vectores de caída de tensión a través de la resistencia y el inductor. AE representa la línea de referencia actual. AB representa la caída de voltaje en la resistencia que está en fase con la línea de corriente.
AD representa la caída de tensión inductiva que conduce la corriente en 900. La resultante de estos vectores da la tensión total a través del circuito.
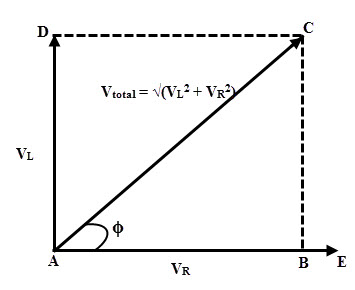
La figura siguiente muestra el diagrama vectorial del circuito de la serie RL que consiste en vectores de caída de tensión entre resistencia e inductor. AE representa la línea de referencia actual. AB representa la caída de tensión en la resistencia que está en fase con La línea de corriente AD representa la caída de tensión inductiva que conduce la corriente en 900. La resultante de estos vectores da la tensión total a través del circuito.
Aplicando el teorema de Pitágoras sobre el triángulo de voltaje, obtenemos
Vtotal = √ (VL2 + VR2)
tan∅ = VL/VR
Sabemos que VR = I × R y VL = I × XL
Mediante estas ecuaciones podemos reescribir el Vtotal como
Vtotal = √ ((I × R) 2+ (I × XL) 2)
I = V/√ ((R) 2+ (XL) 2) = V/Z (Amperios)