Contenido
Introducción
La corriente alterna cambia su dirección periódicamente. Depende del tiempo. Podemos explicar y comprender las características trazando los valores instantáneos de la corriente alterna. Esta trama de forma de onda se denomina ‘forma de onda de CA’. Para medir los diferentes parámetros de la forma de onda de CA hay diferentes métodos. Todo esto se explica en su tutorial.
Valor máximo de una forma de onda de CA
El valor máximo de un medio ciclo positivo o un medio ciclo negativo se denomina «Valor máximo». Está representado por Im. Es el voltaje máximo alcanzado por la onda de CA.
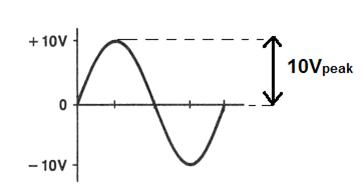
Peak-to-Valor máximo
» Peak-a-pico » voltaje es el voltaje medido entre las amplitudes máxima positiva y negativa de una onda sinusoidal. Es el doble de la amplitud de la forma de onda de CA. Este es el valor de voltaje máximo de la forma de onda. Se denota por VPK.
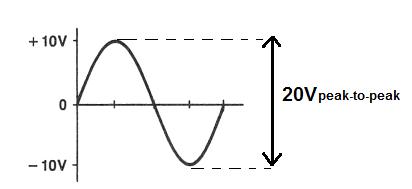
Valor promedio
Este es el promedio de todos los valores de un medio ciclo de una onda de CA. Para encontrar el valor promedio de una forma de onda alterna, un medio ciclo se divide en ordenadas equiespaciadas. Al calcular la tensión promedio de estos valores instantáneos de voltaje obtenemos el valor promedio de la forma de onda de CA. Es el cociente del área bajo la forma de onda con respecto al tiempo.
El valor promedio es 0.637 veces el valor pico a pico.
VAV = VPK x 0.637

Podemos calcular el valor promedio mediante la fórmula dada a continuación.
VAV = (Suma de todas las ordenadas medias)/(Número de intermediarios)
VAV = V1 + V2 + V3 +——+ Vn/n
Voltaje RMS
Esto significa Root Mean Square y es el forma estándar de medir y reportar corriente alterna y voltaje. El RMS se puede calcular multiplicando el voltaje de pico a pico por la raíz cuadrada de 2 (aproximadamente 0,707).
VRMS = VPK x 0,707
El valor RMS se define como la «raíz cuadrada de los promedios de los cuadrados de todos los voltajes en la forma de onda».
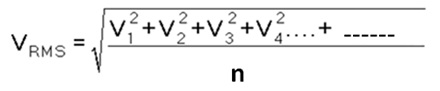
El valor RMS es el método más comúnmente utilizado para representar el voltaje de una forma de onda Ac.
El valor RMS se puede representar en la forma de otros voltajes,
VRMS = Vpeak x 1/2
VRMS = V pico a pico x 1/22
VRMS = Vavg x π/22
Importancia del valor RMS
En el caso de las corrientes alternas, las magnitudes de la corriente se expresan en forma de valores RMS.
En general, solíamos decir que el la corriente de retención de la casa es de 120 voltios de corriente alterna. Esto realmente significa que la tensión RMS de la potencia de retención de la casa es de 120 V.
El calor producido en la bobina, debido al flujo de corriente alterna, es proporcional al cuadrado del valor RMS de la corriente.
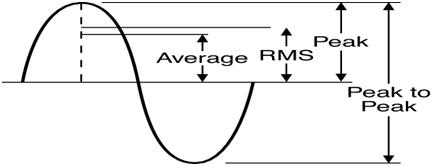
Podemos mida la tensión RMS con todos los voltímetros. En algunos voltímetros costosos, primero se calcula el voltaje pico y luego multiplicándolo por 0,707, obtenemos el valor de voltaje RMS, con mayor precisión.
Factor de forma y factor de cresta
Factor de forma
«El factor de forma es la relación entre el valor de voltaje RMS de una onda alterna y su voltaje promedio». Esto se representa por Kf.
Factor de forma = voltaje RMS/voltaje promedio
Kf = Vrms/Vavg
Por el relación entre el valor promedio de voltaje y el valor RMS, podemos calcular el factor de forma como
Kf = 0.707 Vmax/0.637 Vmax
= 1.11
Factor de cresta
» El factor de cresta es la relación entre el valor de voltaje máximo y su valor de voltaje RMS «. El factor de cresta también se conoce como «factor máximo» & amp; «Factor de amplitud».
Esto se representa mediante Kp.
Factor de forma = Voltaje máximo/Voltaje RMS
Kp = Vpeak/Vrms
Por la relación entre el valor máximo y el valor RMS, podemos calcular el factor de Crest como
Kp = Vmax/0.707 Vmax
= 1.414
Ejemplo
Averigüe todas las medidas de CA de una ola con 10 Amplitud V y frecuencia de 20 Hz y valor promedio de 6.3v.
Sol:
Dado que el valor máximo es 10
El voltaje de pico a pico es = 2 x voltaje de pico
= 2 x 10
= 20 voltios
Periodo de tiempo = 1/f
= 1/20
= 0.05 seg
Valor de tensión RMS = Vpeak x 0.707
= 10 x 0.707
= 7.07 V
Velocidad angular (ω) = 2π f (rad/s)
= 2 x 3.1416 x 20
= 125.6 rad/seg
Factor de forma Kf = Vrms/Vavg
= 7.07/6.3
= 1.11
Factor de Crest Kp = Vpeak/Vrms
= Vmax/0.707 Vmax
= 10/(0.707 x 10 )
= 1.414
Tabla de conversión de medidas
Al usar el factor de forma y el factor de cresta, al usar el valor RMS y los valores promedio de las olas podemos descubrir la forma de una forma de onda. Pero a veces nos confundiremos al convertir varias formas de onda sinusoidales. La tabla que se proporciona a continuación nos ayudará a convertir un valor de onda sinusoidal en otro.
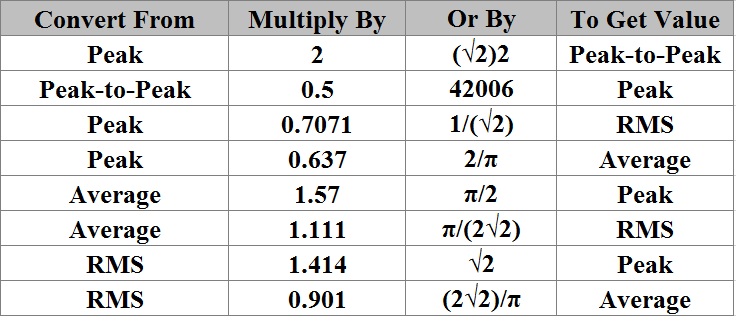
Volver arriba
Relación Entre la frecuencia y el tiempo periódico
La frecuencia de una forma de onda se define como «El número de ciclos por segundo». Esto significa el número de compl. ete oscilaciones realizadas por una onda alterna, en un segundo «.
Frecuencia (f) = 1/Periodo de tiempo
Las unidades son hercios.
Como el período de tiempo y la frecuencia son recíprocos entre sí, podemos definir el período de tiempo como» El inverso de la frecuencia «.
Periodo de tiempo (t) = 1/frecuencia
Las unidades son segundos y milisegundos.
Algunas conversiones estándar entre frecuencia y tiempo
- 1 KHz (Kilohertz) = 1 ms (milisegundos)
- 1 MHz (Megahertz) = 1 us (microsegundos)
- 1 GHz (Gigahertz) = 1 ns (nanosegundos)
- 1 THz (Terahercios) = 1 ps (picosegundos)
Ejemplo
¿Calcula la hora periódica de la señal de CA cuya frecuencia es 60 Hz?
Sol: el tiempo de la señal de CA es T = 1/f
Dada la frecuencia de la señal f = 60 Hz
Periodo de tiempo (T) = 1/f
= 1/60 seg
= 0.01666 sec
= 16.66 ms (milisegundos)
El período de tiempo de la forma de onda es de 16.66 ms.