Contenido
- 1 Introducción
- 2 Passive Band Pass filter
- 3 Filtro de paso de banda con componentes R, L y C
- 4 Respuesta de frecuencia del filtro pasa banda
- 5 Frecuencia central del filtro de paso de banda
- 6 Ejemplo de filtro de paso de banda
- 7 Resumen del filtro de paso de banda pasiva
- 8 Aplicaciones del filtro de paso de banda
Introducción
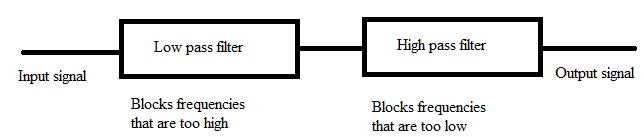
Podemos decir que un filtro de paso de banda es una combinación de filtro de paso bajo y filtro de paso alto. El nombre del filtro en sí indica que solo permite una cierta banda de frecuencias y bloquea todas las frecuencias restantes. En aplicaciones de audio, a veces es necesario pasar solo un cierto rango de frecuencias, este rango de frecuencia no comienza en 0Hz o termina a una frecuencia muy alta, pero estas frecuencias están dentro de un cierto rango, ya sea ancho o estrecho. Estas bandas de frecuencias se denominan comúnmente Bandwidth.
& nbsp;
Passive Band Pass filter
El filtro de paso de banda se obtiene mediante la transferencia en cascada de los filtros de paso pasivo pasivos y paso bajo pasivos. Esta disposición proporcionará un filtro selectivo que pasa solo ciertas frecuencias. Este nuevo circuito de filtro RC puede pasar ya sea un estrecho rango de frecuencias o un amplio rango de frecuencias. Este rango de frecuencias de paso que es estrecho o amplio dependerá de la forma en que pasen los pases bajos y la cascada del filtro de paso alto. Las frecuencias de corte superior e inferior dependen del diseño del filtro. Este filtro de paso de banda simplemente aparece como un filtro selectivo de frecuencia.
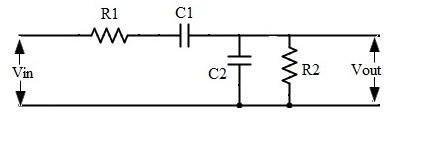
La figura de arriba muestra el Circuito de filtro de paso de banda. La entrada dada es una señal sinusoidal. Las propiedades de las combinaciones de pase bajo y paso alto nos dan el filtro de paso de banda. Al organizar un conjunto de elementos de RC en serie y otro conjunto de elementos de RC en paralelo, el circuito se comporta como un filtro de paso de banda. Esto nos da un filtro de segundo orden porque el circuito tiene dos componentes reactivos. Un condensador pertenece al filtro de paso bajo y otro capacitor pertenece al filtro de paso alto. Sin variaciones en la señal de entrada, este filtro de paso de banda pasará un cierto rango de frecuencias. Este filtro no produce ningún ruido extra en la señal. La frecuencia de corte del circuito se puede calcular de la siguiente manera
fC = 1/(2πRC)
Ajustando el corte de las frecuencias de los filtros de paso alto y paso bajo, podemos obtener el ancho apropiado de la banda de paso para el filtro de paso de banda.
). empujar({ );
Como este filtro pasa una banda de frecuencias, este filtro contiene dos frecuencias de corte, una frecuencia de corte más baja ‘fL & # 8216; y una frecuencia de corte más alta ‘fH’. Por lo tanto, el rango de las frecuencias que pasan a través del filtro se denomina ancho de banda del filtro. En general, el ancho de banda del circuito puede calcularse mediante las frecuencias fH y fL.
BW = fH-fL
Donde,fH es la frecuencia de corte del filtro de paso alto y &fL es la frecuencia de corte del filtro de paso bajo. ‘BW’ es el ancho de banda del filtro. El filtro de paso de banda pasará las frecuencias más altas que la frecuencia de corte del filtro de paso alto y menor que la frecuencia de corte del filtro de paso bajo. Esto muestra que la frecuencia de corte del filtro de paso bajo debe ser mayor que la frecuencia de corte del filtro de paso alto.
Filtro de paso de banda con componentes R, L y C
El diseño del circuito del filtro de paso de banda mediante el uso de un inductor, condensador y resistencia se proporciona a continuación
La frecuencia central del filtro de paso de banda, que también se denomina ‘pico resonante’, se puede formular utilizando la siguiente ecuación.
fc = 1/2π√ (LC)
Donde L = inductancia de un inductor cuyas unidades están en Henry (H).
C = capacitancia de un condensador cuyas unidades están en Farad (F).
También podemos diseñar un filtro de paso de banda con inductores, pero saber tha Debido a la alta reactancia de los condensadores, el diseño del filtro pasa banda con elementos RC es más ventajoso que los circuitos RL.
Respuesta de frecuencia del filtro pasa banda
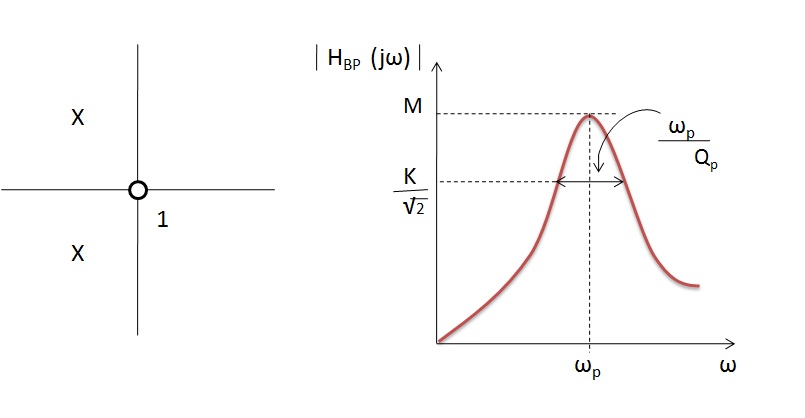

La frecuencia del polo es aproximadamente igual a la frecuencia de la ganancia máxima.
La curva de respuesta de frecuencia del filtro de paso de banda se muestra a continuación: Las características ideales y las características prácticas de los filtros de paso de banda son diferentes debido a la reactancia de entrada del circuito.
La ganancia de la señal de entrada se puede calcular tomando 20 log (Vout/Vin). El rango puede ser bastante grande dependiendo de las características inherentes del circuito. La señal se atenúa a bajas frecuencias con la salida aumentando a una pendiente de +20 dB por década o 6 dB por octava hasta que la frecuencia llegue a una frecuencia de corte más baja ‘fL’. A esta frecuencia, la ganancia de la señal alcanza el valor 1/√2 = 70.7%.
Después de la frecuencia de corte fL, la salida aumentará con el aumento de frecuencia con una frecuencia de-20 dB por década y alcanza la ganancia máxima y esta ganancia es constante hasta que alcanza la frecuencia de corte más alta ‘f_H’. Después de la frecuencia de corte más alta, la salida disminuye a una pendiente de-20dB/década o-6dB/octava.
Anteriormente hemos visto que el cambio de fase del filtro de primer orden es de 90 °. Sabemos que el filtro de paso de banda es un filtro de segundo orden, por lo que el cambio de fase es el doble del filtro de primer orden que es de 180 °. El ángulo de fase variará con el aumento de la frecuencia. En la frecuencia central, las señales de salida y entrada están en fase entre sí. Debajo de la frecuencia de resonancia, la señal de salida conduce a la señal de entrada y, por encima de la frecuencia de resonancia, la señal de salida está retrasada. La amplitud de la señal de entrada siempre es mayor que la señal de salida. Para aumentar la ganancia del circuito, el valor de la resistencia R1 debe ser mayor que la resistencia R2.
Frecuencia central del filtro de paso de banda
La «frecuencia central» o «frecuencia resonante» en el cual la ganancia de salida es máxima se puede obtener calculando la media geométrica de las frecuencias de corte superior e inferior.
fr2 = fH x fL
fr = √ (fH x fL)
Donde fr es la frecuencia de resonancia o la frecuencia central
fH-es la frecuencia de corte superior a-3 dB
fL-es la más baja-3 Frecuencia de corte de dB
Ejemplo de filtro de paso de banda
Supongamos que el filtro de paso de banda permitirá las frecuencias de 1 kHz a 30 kHz y contiene una resistencia de 10 kΩ. Al considerar estos valores, podemos calcular la capacitancia del condensador. Ya sabemos que el valor de frecuencia de corte del filtro de paso bajo debe ser mayor que el filtro de paso alto. Entonces, la frecuencia de corte del filtro de paso alto es de 1 kHz y la frecuencia de corte del filtro de paso bajo es de 30 kHz.
En la etapa de filtro de paso alto
fL = 1 kHz y resistencia R = 10 kΩ
C = 1/(2πfLR) = 1/(2 * π * 1000 * 1000) = 15.8 nF
En la etapa de filtro de paso bajo
fH = 30 kHz y Resistencia R = 10 kΩ
C = 1/(2πfHR) = 1/(2 * π * 30000 * 10000) = 510 pF
A partir de los cálculos anteriores, el valor del condensador requerido para el filtro de paso alto es de 15.8 nF y el valor del condensador del filtro de paso bajo es 510 pF.
Resumen del filtro de paso de banda pasiva
El filtro de paso de banda se obtiene conectando en cascada un filtro de pase bajo y paso alto. Es un filtro de segundo orden ya que contiene dos elementos reactivos. El orden del filtro depende del número de circuitos en cascada que se utilizan en el circuito.
La ganancia de la señal de salida es siempre menor que la señal de entrada. En la frecuencia central, la señal de salida está en fase, pero por debajo de la frecuencia central, la señal de salida lidera la fase con un desplazamiento de + 90 ° y por encima de la frecuencia central, la señal de salida se retardará en fase con el cambio de fase de-90 °.
Las características prácticas del pase de banda el filtro es un poco diferente con respecto a las características ideales. Esta variación se debe principalmente a la cascada de filtro de paso alto con filtro de paso bajo. La ganancia de salida siempre es menor que la unidad. Cuando proporcionamos aislamiento eléctrico entre los filtros de paso alto y paso bajo, podemos lograr un mejor rendimiento del filtro.
El filtro de paso de banda optimizará la sensibilidad del receptor. El filtro de paso alto se agrega primero al diseño, luego se agrega el filtro de paso bajo. Aunque si agregamos un filtro de paso bajo primero y luego el filtro de paso alto, nunca hará cambios en la señal de salida. El factor de calidad del filtro dependerá del valor de la resistencia R1. Si R1 es bajo, el factor de calidad es bajo y si el valor R1 es alto, el factor de calidad es alto.
Aplicaciones del filtro de paso de banda
1. Estos se utilizan en el medio de comunicación inalámbrico en los circuitos del transmisor y el receptor. En la sección del transmisor, este filtro pasará las únicas señales requeridas y reducirá la interferencia de señales con otras estaciones. En la sección del receptor, ayudará a la penetración de la señal no deseada en los canales.
2. Estos se utilizan para optimizar la relación señal/ruido del receptor.
3. Estos se utilizan en el área de comunicación óptica como LIDARS.
4. Se usan en algunas de las técnicas de filtrado de color.
5. Estos también se usan en instrumentos médicos de campo como EEG.
6. En aplicaciones telefónicas, en DSL para dividir señales de teléfono y de banda ancha.