Diseño de circuito de filtro de paso alto activo y aplicaciones

 

Introducción

Un filtro de paso alto permitirá frecuencias que son más altas que la frecuencia de corte y atenúan las frecuencias más bajas que la frecuencia de corte. En algunos casos, este filtro también se denomina filtro de «corte bajo» o filtro de «corte de base». La cantidad de atenuación o el rango de banda de paso dependerá de los parámetros de diseño del filtro.

La ganancia de la banda de paso de un filtro activo es mayor que la ganancia unitaria. El funcionamiento del filtro de paso alto activo es el mismo que el filtro pasivo de paso alto, pero la principal diferencia es que el filtro de paso alto activo utiliza un amplificador operacional que proporciona amplificación de las señales de salida y controla la ganancia.

las características ideales del filtro de paso alto se muestran a continuación

Sabemos que el filtro de paso alto pasará las frecuencias desde el punto de frecuencia de corte a la frecuencia ‘infinito’ que no existe en consideraciones prácticas. Además del filtro pasivo de paso alto en este filtro activo de paso alto, la respuesta de frecuencia máxima está limitada por las características de bucle abierto del amplificador operacional.

Filtro activo de paso alto

Al conectar un dispositivo pasivo El circuito de filtro de paso alto RC al terminal inversor o no inversor del amplificador operacional nos proporciona un filtro de paso alto activo de primer orden. El circuito pasivo de filtro de paso alto RC conectado al terminal no inversor del amplificador operacional de ganancia unitaria se muestra a continuación.

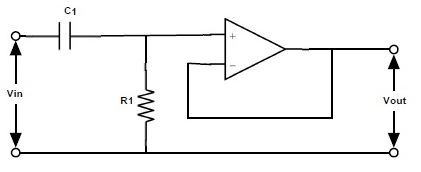
La ganancia Amax = 1 y la frecuencia de corte fc = 1/2πRC

Filtro de paso alto activo con ganancia de alto voltaje

La operación es la misma que la del filtro pasivo de paso alto, pero la señal de entrada se amplifica mediante el amplificador en la salida. La cantidad de amplificación depende de la ganancia del amplificador. La magnitud de la ganancia de la banda de paso es igual a 1 + (R3/R2). Donde R3 es la resistencia de retroalimentación en Ω (ohmios) y R2 es la resistencia de entrada. El circuito del filtro activo de paso alto con amplificación se proporciona a continuación

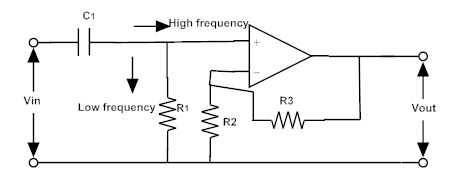
Ganancia de voltaje de un filtro de paso alto activo

Ganancia de voltaje Av = Amax (f/fc)/√ {1 + (f/fc) ²

Wheref = frecuencia de operación

fc = frecuencia de corte

Amax = ganancia de la banda de paso del filtro = 1 + (R3/R2)

A bajas frecuencias significa cuando la frecuencia de operación es menor que la frecuencia de corte, la ganancia de voltaje es menor que la ganancia de la banda de paso Amax. A altas frecuencias significa que cuando la frecuencia de operación es mayor que la frecuencia de corte, la ganancia de voltaje del filtro es igual a la ganancia de banda de paso. Si la frecuencia de operación es igual a la frecuencia de corte, entonces la ganancia de voltaje del filtro es igual a 0.707 Amax.

Aumento de voltaje en (dB)

La magnitud de la ganancia de voltaje generalmente se toma en decibelios (dB ):

Av (dB) = 20 log10 (Vout/Vin)

-3 dB = 20 log10 (0.707 * Vout/Vin)

La frecuencia de corte que separa tanto la banda de paso como la de stop se puede calcular usando la fórmula siguiente fC = 1/(2πRC)

El desplazamiento de fase del filtro de paso alto activo es igual al del filtro pasivo. Es igual a + 45 ° en la frecuencia de corte fC y este valor de desplazamiento de fase se equipara como

Ø = tan-1 (1/2πfcRC)

Respuesta de frecuencia del filtro de paso alto activo

La curva de respuesta de frecuencia con respecto a la ganancia de lazo abierto de los amplificadores se muestra a continuación.

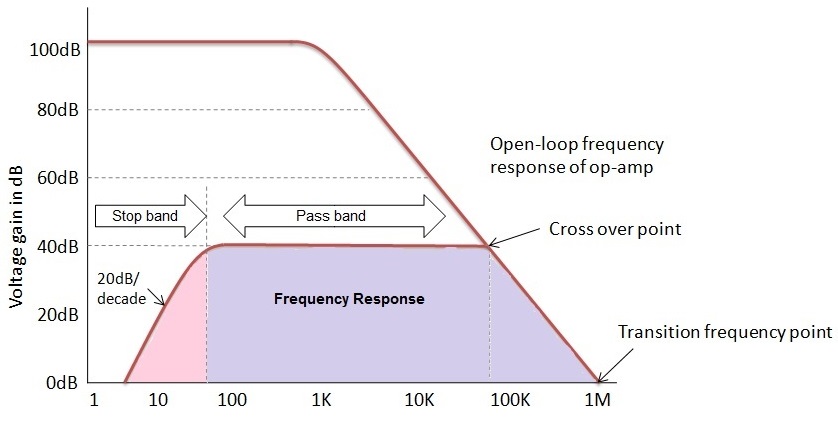
En la respuesta de frecuencia del filtro de paso alto activo, la frecuencia máxima de banda de paso está limitada por las características de ancho de banda o bucle abierto de el amplificador operacional. Debido a esta limitación, la respuesta del filtro de paso alto activo aparecerá como la respuesta del filtro de banda ancha. Al utilizar este filtro de paso alto activo basado en el amplificador operacional, podemos lograr una alta precisión con el uso de resistencias y condensadores de baja tolerancia.

Filtro de paso alto activo utilizando un amplificador operacional de inversión

que el filtro de paso alto activo se puede diseñar usando cualquiera de los terminales de inversión o el terminal no inversor de un amplificador operacional. Hasta ahora vimos el circuito de filtro de paso alto y las curvas de respuesta del filtro de paso alto activo no inversor. Ahora veamos el filtro de paso alto activo usando el op-amp inversor.

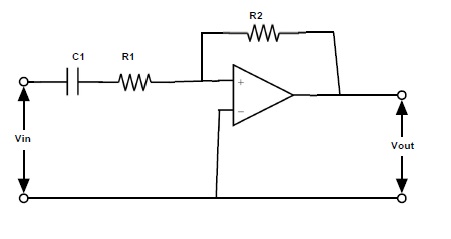
Derivación de ganancia en forma de Laplace

Consideremos el amplificador inversor como se muestra a continuación

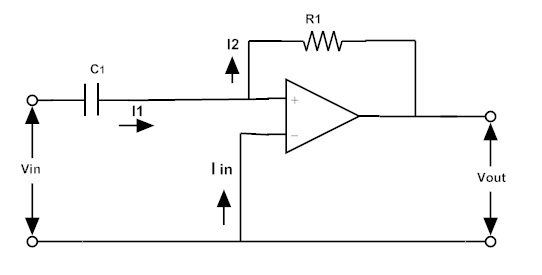
La impedancia de entrada Z1 = 1/sC1

Donde s = Laplace Variable

C1 = Capacitancia

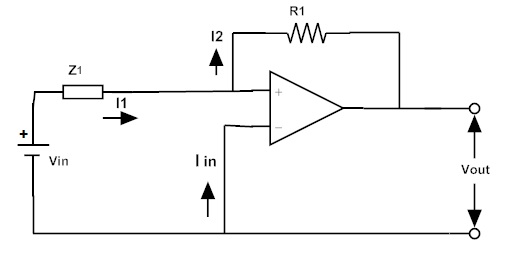
Las corrientes que circulan en el circuito son I1, I2 e Iin,

Donde I1 = I2 e Iin = 0

Vin/Z1 =-Vout/R1

Vout/Vin =-R1/Z1

Vout/Vin =-R1/(1/sC1)

Vout/Vin =-sR1C1 = Ganancia

Ejemplo de filtro de paso alto activo

Consideremos el valor de frecuencia de corte como 10 KHz, pase la ganancia de banda Amax como 1.5 y el valor del condensador como 0.02 μF

La ecuación de la frecuencia de corte es fC = 1/(2πRC)

Reordenando esta ecuación tenemos R = 1/(2πfC)

R = 1/(2π * 10000 * 0.02 * 10-6) = 795.77 Ω

La ganancia de banda de paso del filtro es Amax = 1 + (R3/R2) = 1.5

R3 = 0.5 R2

Si consideramos el valor de R2 como 10KΩ, entonces R3 = 5 kΩ

Podemos calcular la ganancia del filtro de la siguiente manera

Aumento de voltaje para filtro de paso alto | Vout/Vin | = Amax * (f/fc)/√ [1 + (f/fc) ²]

Av (dB) = 20 log10 (Vout/Vin)

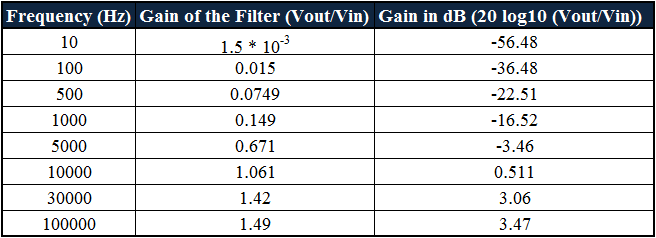
Usando esta ecuación, tabulemos las respuestas para el rango de frecuencias para trazar la curva de respuesta del filtro. Estas respuestas se suponen de 10 Hz a 100 KHz.

Bode-plot

Para analizar la respuesta de frecuencia del circuito, este diagrama de bode es usado. No es más que un gráfico de la función de transferencia de la frecuencia de versos lineales, variantes de tiempo. Esto se traza con el eje de frecuencia de registro. Consiste principalmente en dos parcelas; una es una gráfica de magnitud y la otra es una gráfica de fase.

La gráfica de magnitud expresará la magnitud de la respuesta de frecuencia, es decir, la ganancia y la gráfica de fase se usa para expresar la respuesta del cambio de frecuencia.

El diagrama de bode de respuesta de frecuencia de acuerdo con los valores que se tabulan arriba se proporciona a continuación:

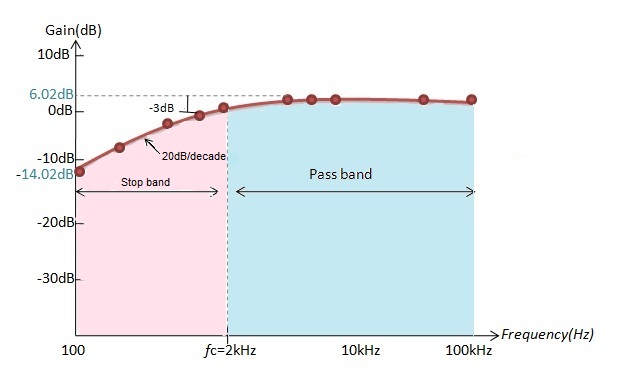
Según los valores calculados, a una frecuencia de 10 Hz, la ganancia del filtro obtenida en dB es-56,48. Si aumentamos el valor de la frecuencia a 100 Hz, la ganancia obtenida es-36.48 dB y, a una frecuencia de 500 Hz, la ganancia del filtro es-22.51 dB, a una ganancia de frecuencia de 1000 Hz en dB es-16.52. Por esto podemos decir que si la frecuencia aumenta la ganancia del filtro aumenta a una velocidad de 20 dB/década.

Hasta la frecuencia de corte de 10 KHz aumenta la ganancia del filtro, pero después de la frecuencia de corte la ganancia alcanza el valor máximo y es constante.

Filtro de paso alto de segundo orden

La respuesta de frecuencia del filtro activo de segundo orden es exactamente opuesta a la respuesta del filtro de paso bajo activo de segundo orden porque este filtro atenuará los voltajes debajo del frecuencia de corte. La función de transferencia del filtro de segundo orden se da a continuación

Vout (s)/Vin (s) =-Ks²/s² + (ω0/Q) s + ω0²

Donde K = R1/R2 y ω0 = 1/CR

Esta es la forma general del filtro de paso alto de segundo orden.

Circuito de filtro de paso alto activo de segundo orden

El procedimiento de diseño para el filtro activo de segundo orden es el mismo que el filtro de primer orden porque la única variación está en el balanceo. Si la caída del filtro de paso alto activo de primer orden es de 20dB/década, entonces el balanceo del filtro de segundo orden es de 40 dB/década. Significa el doble del valor del filtro de primer orden. El circuito del filtro de segundo orden se muestra a continuación

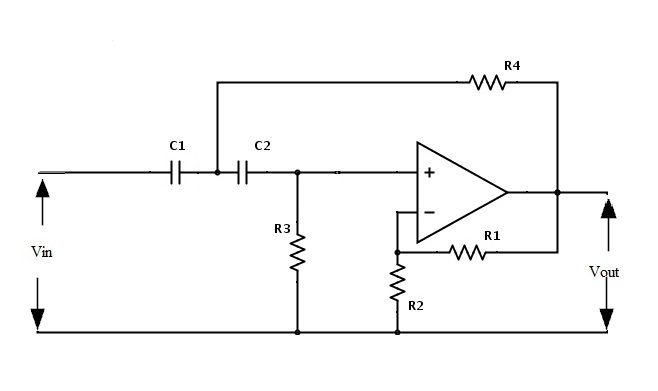
La ganancia del filtro es 1+ R1/R2 y la ecuación de la frecuencia de corte es fc = 1/2π√R3R4C1C2

Ejemplo de filtro de paso alto activo de segundo orden

Vamos a diseñar un filtro con una frecuencia de corte de 4 KHz y la tasa de retardo en la banda de parada es de 40 dB/década. Como la velocidad de retardo en la banda de parada es de 40 dB/década, podemos decir claramente que el filtro es de segundo orden.

Consideremos los valores del condensador como C1 = C2 = C = 0.02μF

La ecuación de la frecuencia de corte es R = 1/2πfC

Reordenando esta ecuación tenemos R = 1/2πfC

Sustituyendo los valores de la frecuencia de corte como 4 KHz y el condensador como 0.02μF

R = 1.989 KΩ = 2 KΩ.

Deje que la ganancia del filtro sea 1+ R1/R2 = 2

R1/R2 = 1

R1 = R2

Por lo tanto, podemos tomar R1 = R2 = 10 KΩ

Por lo tanto, el filtro obtenido se muestra a continuación

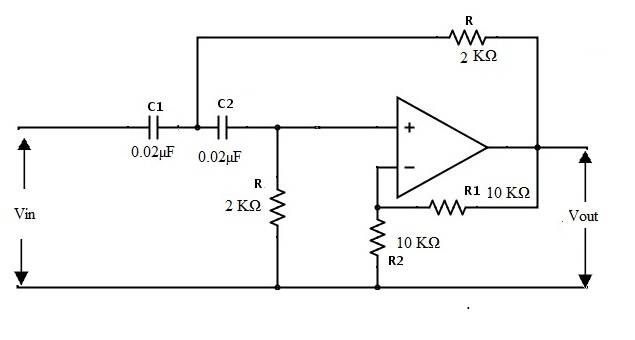
Filtros de paso alto de orden superior

Al poner en cascada el filtro de primer orden con filtro de segundo orden, podemos obtener el tercer orden filtrar. Cuando colocamos en cascada dos filtros de segundo orden, podemos obtener el filtro de cuarto orden. Así, con la ayuda de los filtros de primer orden y de segundo orden, obtenemos los filtros de orden superior.

Con el aumento en el orden del filtro, la diferencia entre la banda de parada real y la banda de detención teórica aumenta. Pero la ganancia total del filtro de orden superior es igual porque ya vimos que las resistencias y los condensadores que determinan los valores de respuesta de frecuencia serán los mismos.

Este orden en cascada se muestra a continuación

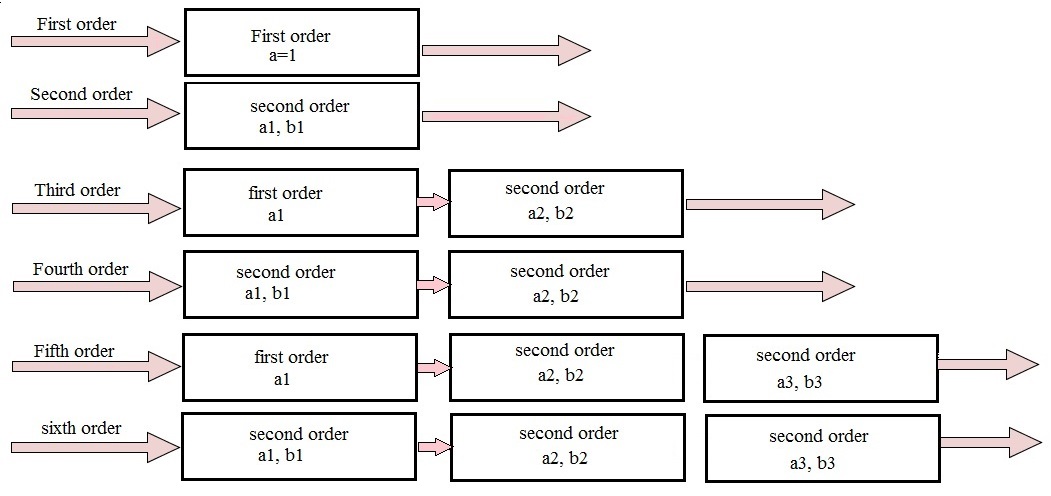
Aplicaciones de filtros de paso alto activos

• Se utilizan en los altavoces para reducir el nivel bajo de ruido.
• Elimina las distorsiones estruendosas en las aplicaciones de audio, por lo que también se denominan filtros de refuerzo de agudos.
• Se utilizan en amplificadores de audio para amplificar las señales de frecuencia más altas.
• También se usan en ecualizadores.