Contenido
Introducción
Muchos de los circuitos eléctricos son de naturaleza compleja y los cálculos requeridos para encontrar las cantidades desconocidas en tales circuitos, usando la ley de ohmios simple y los métodos de simplificación de combinación serie/paralelo no son posibles. Por lo tanto, para simplificar estos circuitos, se usan las leyes de Kirchhoff. Estas leyes son las herramientas analíticas fundamentales que se utilizan para encontrar las soluciones de tensiones y corrientes en un circuito eléctrico, ya sea que se trate de CA o CC. Los elementos en un circuito eléctrico se conectan de numerosas maneras posibles, por lo tanto, para encontrar los parámetros en un circuito eléctrico, estas leyes son muy útiles.
Antes de ir a conocer mas sobre la ley de Kirchhoff, debemos considerar algunos de los términos relacionados con los circuitos eléctricos.
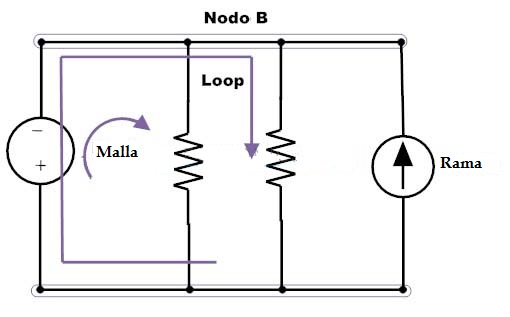
Nodo: Nodo o unión es un punto en el circuito donde dos o más elementos eléctricos están conectados. Esto especifica un nivel de voltaje con un nodo de referencia en un circuito.
Rama: El camino continuo de conducción entre dos uniones que contiene un elemento eléctrico en un circuito se denomina rama.
Loop: en un circuito eléctrico, un loop es una ruta cerrada independiente en un circuito que sigue la secuencia de ramas de tal manera que debe comenzar y terminar con el mismo nodo y no debería tocar ninguna otra unión o nodo más de una vez.
Malla: en un circuito eléctrico, la malla es un bucle que no contiene ningún otro bucle en su interior.
Volver arriba
Leyes de Kirchhoff
En 1847, Gustav Robert Kirchhoff, un físico alemán desarrolló estas leyes para describir el voltaje y la relación actual en un circuito eléctrico. Estas leyes son: Ley de Voltaje de Kirchhoff & (KVL) y Ley la corriente de Kirchhoff (KCL).
Ley de la corriente de Kirchhoff
Esta también se conoce como la ley de conservación de carga porque la carga o la corriente no pueden crearse o destruirse en la unión o nodo. Establece que la la suma algebraica de las corrientes en cualquier nodo es cero. Por lo tanto, la corriente que ingresa en un nodo debe ser igual a la suma de corriente fuera del nodo.
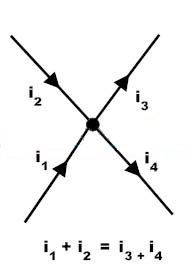
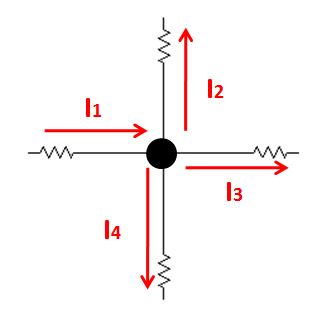
En la figura anterior, las corrientes I1 e I2 están ingresando al nodo mientras que las corrientes I3 a nd I4 se están yendo del nodo. Al aplicar KCL en el nodo, supongamos que las corrientes de entrada son positivas y las corrientes de salida son negativas, podemos escribir como
I1 + I2 + (-I3) + (-I4) = 0 I1 + I2 = I3 + I4
Problema de ejemplo de KCL
Considere la siguiente figura donde tenemos que determinar las corrientes IAB e Ix usando KCL.
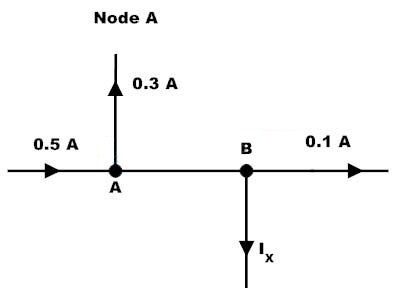
Aplicando Kirchhoff ’ s Ley actual en el punto A, obtenemos
IAB = 0.5-0.3
IAB = 0.2 Amps
Del mismo modo, al aplicar KCL en el punto B, obtenemos
IAB = 0.1 + Ix
0.2 = 0.1 + Ix
Ix = 0.2-0.1 = 0.1 Amps
Ley de voltaje de Kirchhoff
La Ley de Voltaje de Kirchhoff establece que la suma algebraica de voltajes en un camino cerrado es igual a cero, que es la suma de los voltajes de fuente igual a la suma de las caídas de voltaje en un circuito. Si la corriente fluye de mayor potencial a menor en un elemento, entonces lo consideramos como una caída de voltaje. Si la corriente fluye de menor potencial a mayor potencial, entonces lo consideramos como un aumento de voltaje. Por lo tanto, la energía disipada por la corriente debe ser igual a la energía dada por la potencia suministro en un circuito eléctrico.
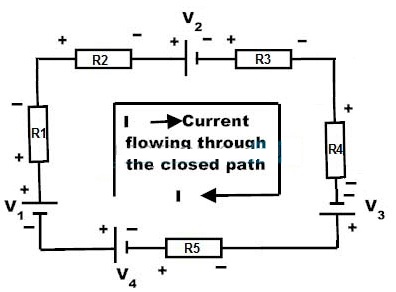
Considere el circuito de arriba donde la dirección del flujo de corriente se toma en el sentido de las agujas del reloj. Las caídas de tensión en el circuito anterior son V1 es positivo, IR1 es negativo (caída de tensión), IR2 es negativo (caída de tensión), V2 es negativo, IR3 es negativo (caída de tensión), IR4 es negativo (caída de tensión), V3 es positivo, IR5 es negativo y V4 es negativo. Al aplicar KVL, obtenemos
V1 + (-IR1) + (-IR2) + (-V2) + (-IR3) + (-IR4) + V3 + (-IR5) + (-V4) = 0
V1-IR1-IR2-V2-IR3-IR4 + V3-IR5-V4 = 0
V1-V2 + V3 y # 8211; V4 = IR1 + IR2 + IR3 + IR4 + IR5
Por lo tanto, la KVL también se conoce como la ley de conservación de la energía eléctrica porque la suma de las caídas de tensión (producto de resistencia y corriente) es igual a la suma de las fuentes de voltaje en una ruta cerrada.
Ejemplo de ley de voltaje de Kirchhoff
1. Consideremos el circuito de bucle único que se muestra a continuación y asumamos la dirección del flujo de corriente como ruta cerrada de DEABCD. En este circuito, al usar KVL tenemos que encontrar el voltaje V1.
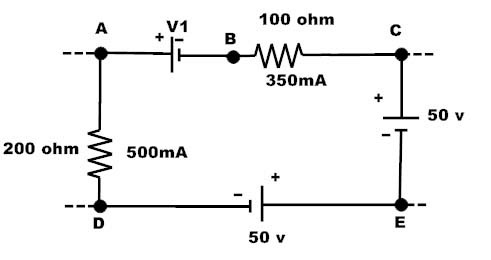
Al aplicar KVL a este ciclo cerrado, puede escribir como
VED + VAE + VBA + VCB + VDC = 0
Donde
Voltaje del punto E con respecto al punto D, VED =-50 V
Voltaje del punto D con respecto al punto C, VDC =-50 V
Voltaje del punto A con respecto al punto E. VAE = I * R
VAE = 500m * 200
VAE = 100 V
Voltaje similar en el punto C con respecto a la pinta B, VCB = 350 m * 100
VCB = 35V
Considere la tensión en el punto A con respecto al punto B, VAB = V1
VBA =-V1
Luego, usando KVL
-50 + 100-V1 + 35-50 = 0
V1 = 35 voltios
2. Considere el siguiente circuito típico de dos bucles donde tenemos que encontrar las corrientes I1 e I2 aplicando las leyes de Kirchhoff.
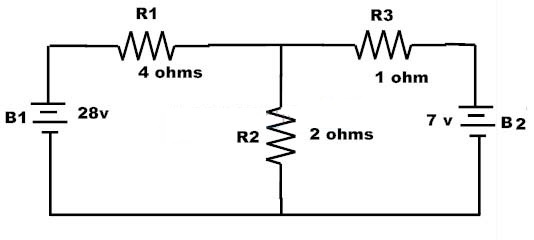
Hay dos bucles dentro del circuito y considerar las rutas de bucle como se muestra en la figura.
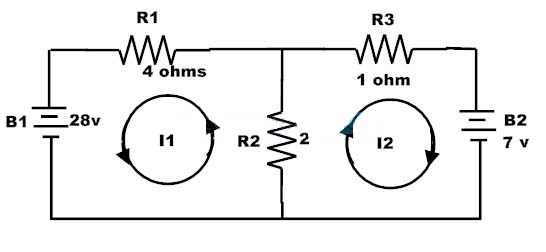
Aplicando KVL a estos loops obtenemos
Para el primer ciclo,
2 (I1 + I2) + 4I1-28 = 0
6I1 + 2I2 = 28 & # 8212; & # 8212; & # 8212; (1)
Para el segundo ciclo,
-2 ( I1 + I2)-1I2 + 7 = 0-2I1-3I2 =-7 y # 8212; & # 8212;-(2)
Al resolver las ecuaciones 1 y 2 anteriores obtenemos,
I1 = 5A e I2 =-1 A
Problema del ejemplo en las leyes de Kirchhoff
Ahora usemos las leyes actuales y de voltaje de Kirchhoff para encontrar las caídas de corriente y voltaje en el circuito inferior. Similar al problema anterior, este circuito también contiene dos bucles y dos uniones. Considere la dirección actual dada en la figura.
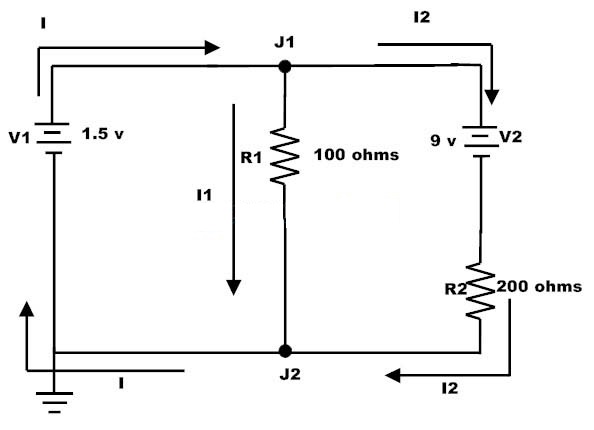
Aplica la ley actual de Kirchhoff en ambos cruces, luego obtenemos
En el cruce 1, I = I1 + I2
En el cruce 2, I1 + I2 = I
Aplique la ley de voltaje de Kirchhoff a los dos bucles, luego obtenemos
En el primer ciclo,
1.5 V-100 I1 = 0
I1 = 1.5/100
= 0.015 Amps
En el segundo ciclo
100 (I1-I2)-9V-200I2 = 0
100I1-300I2 = 9
Sustituyendo el valor I1 en la ecuación anterior, luego
1.5-300I2 = 9
-300I2 = 7.5
I2 =-0.025
Luego la corriente en el cruce I = I1 + I2
I = 0.015-0.025
I =-0.01
Aplicaciones de las Leyes de Kirchhoff ’ s
- Al usar estas leyes, podemos encontrar las resistencias, tensiones y corrientes desconocidas (dirección y valor).
- En el método de bifurcación, encontrar las corrientes a través de cada una de las ramas transportada aplicando KCL en cada unión y KVL en cada bucle de un circuito.
- En el método de corriente de bucle, encontrar corriente a través de cada bucle independiente se realiza aplicando KVL para cada bucle y contando todas las corrientes en cualquier elemento de un circuito.
- Se usa en el método nodal para encontrar voltajes y corrientes.
- Estas leyes se pueden aplicar para analizar cualquier circuito independientemente de la composición y estructura del mismo.