Contenido
- 1 Introducción
- 2 Declaración de teorema máximo de transferencia de energía
- 3 Prueba del teorema de transferencia máxima de potencia
- 4 Eficiencia de transferencia de energía
- 5 Teorema de máxima transferencia de energía para circuitos de CA
- 6 Aplicación del ejemplo de transferencia máxima de potencia al circuito de CC
- 7 Aplicación de la transferencia de energía máxima al circuito de CA
- 8 Aplicación práctica del teorema de máxima transferencia de energía
Introducción
En cualquier circuito eléctrico, la energía eléctrica del suministro se entrega a la carga donde se convierte en un trabajo útil. Prácticamente, toda la potencia suministrada no se presentará en la carga debido al efecto de calentamiento y otras restricciones en la red. Por lo tanto, existe una cierta diferencia entre el dibujo y la entrega de poderes.
El tamaño de la carga siempre afecta la cantidad de energía transferida desde la fuente de suministro, es decir, cualquier cambio en la resistencia de carga resulta en cambios en la transferencia de potencia a la carga. Por lo tanto, el teorema de transferencia de potencia máxima asegura la condición de transferir la potencia máxima a la carga. Veamos cómo.
Declaración de teorema máximo de transferencia de energía
El teorema de transferencia de potencia máxima establece que en una red DC bilateral lineal, la potencia máxima se entrega a la carga cuando la resistencia de carga es igual a la resistencia interna de una fuente.
Si se trata de una tensión independiente fuente, luego su resistencia en serie (resistencia interna Rs) o si es fuente de corriente independiente, entonces su resistencia paralela (resistencia interna Rs) debe ser igual a la resistencia de carga RL para entregar la máxima potencia a la carga.
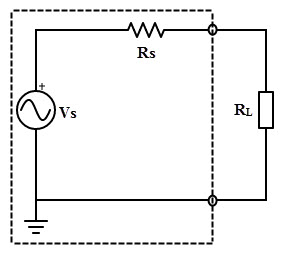
Prueba del teorema de transferencia máxima de potencia
El teorema máximo de transferencia de potencia asegura el valor de la resistencia de carga, a la que se transfiere la potencia máxima a la carga.
Considere la siguiente red de dos terminales de CC (circuito del lado izquierdo), a la cual se determina la condición para la potencia máxima, obteniendo la expresión de potencia absorbida por carga con el uso de malla o métodos de corriente nodal y luego deriva la expresión resultante con respecto a la resistencia a la carga RL.
Pero este es un procedimiento bastante complejo. Pero en artículos anteriores hemos visto que la parte compleja de la red puede reemplazarse con un equivalente de Thevenin como se muestra a continuación.
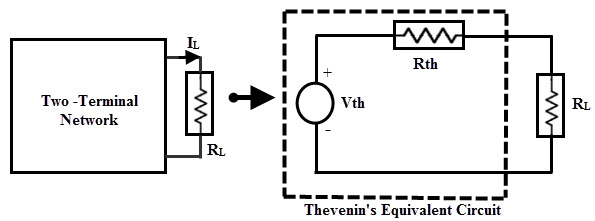
El circuito de dos terminales original se reemplaza con un circuito equivalente de Thevenin a través de la resistencia de carga variable. La corriente a través de la carga para cualquier valor de resistencia a la carga es
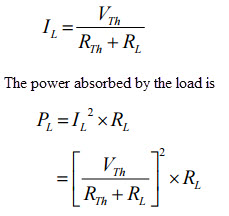
Forma la expresión anterior, la potencia entregada depende de los valores de RTH y RL. Sin embargo, el equivalente de Thevenin es constante, la potencia entregada desde esta fuente equivalente a la carga depende completamente de la resistencia de carga RL. Para encontrar el valor exacto de RL, aplicamos diferenciación a PL con respecto a RL y equiparándolo a cero como
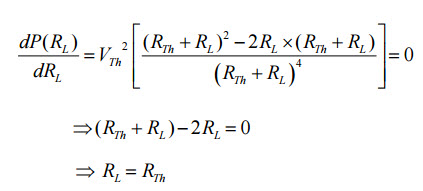
Por lo tanto, esta es la condición de igualar la carga donde ocurre la máxima transferencia de potencia cuando la resistencia de carga es igual a la resistencia de Thevenin del circuito. Sustituyendo la Rth = RL en la ecuación 1 obtenemos
La potencia máxima entregada a la carga es
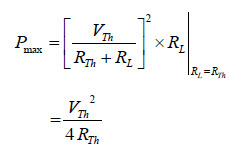
La potencia total transferida desde la fuente es
PT = IL2 (RTH + RL)
= 2 IL2 RL … … … … …. (2)
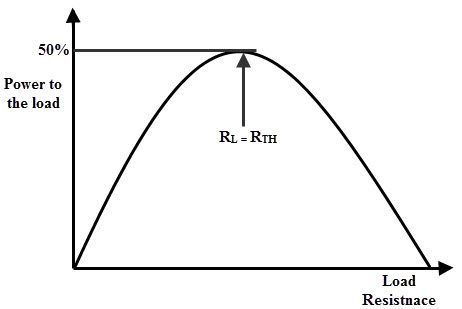
Por lo tanto, el máximo El teorema de transferencia de potencia expresa el estado en el que se entrega la potencia máxima a la carga, es decir, cuando la resistencia de carga es igual a la resistencia equivalente del Thevenin del circuito. La figura siguiente muestra una curva de potencia entregada a la carga con respecto a la resistencia de carga.
Tenga en cuenta que la potencia entregada es cero cuando la resistencia de carga es cero ya que no hay caída de tensión en la carga durante esta condición. Además, la potencia será máxima cuando la resistencia de carga sea igual a la resistencia interna del circuito (o la resistencia equivalente de Thevenin). Nuevamente, la potencia es cero ya que la resistencia de carga llega al infinito ya que no hay flujo de corriente a través de la carga.
Eficiencia de transferencia de energía
Debemos recordar que este teorema resulta en una transferencia de potencia máxima, pero no en una eficiencia máxima. Si la resistencia de carga es menor que la resistencia de la fuente, la potencia disipada con la carga se reduce mientras que la mayor parte de la potencia se disipa en la fuente, entonces la eficiencia disminuye.
Considere la potencia total entregada por la ecuación fuente (ecuación 2), en la cual la potencia se disipa en la resistencia equivalente de Thevenin RTH por la fuente de tensión VTH.
Por lo tanto, la eficiencia bajo la condición de máxima transferencia de potencia es
Eficiencia = Salida/Entrada × 100
= IL2 RL/2 IL2 RL × 100
= 50%
Por lo tanto, en la condición de máxima transferencia de energía, la eficiencia es 50%, eso significa que un medio porcentaje de potencia generada se entrega a la carga y en otras condiciones se entrega un pequeño porcentaje de potencia a la carga, como se indica en eficiencia. transferencia de energía del cu a continuación.
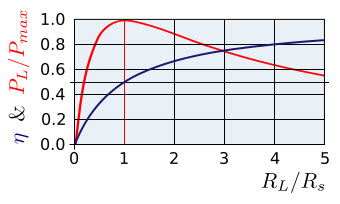
Para algunas aplicaciones, es conveniente transferir máxima potencia para la carga que para lograr una alta eficiencia como en amplificadores y circuitos de comunicación.
Por otro lado, es deseable lograr una mayor eficiencia que la transferencia de potencia maximizada en el caso de sistemas de transmisión de potencia donde una gran carga resistencia (valor mucho más grande que la resistencia de la fuente interna) se coloca a través de la carga. Aunque la eficiencia es alta, la potencia entregada será menor en esos casos.
Teorema de máxima transferencia de energía para circuitos de CA
Puede afirmarse que, como en una red activa, la potencia máxima se transfiere a la carga cuando la impedancia de carga es igual al complejo conjugado de una impedancia equivalente de una red dada vista desde los terminales de carga.
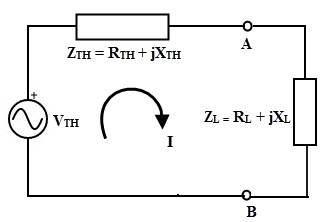
Considere el circuito equivalente de Thevenin anterior a través de los terminales de carga en el que la corriente que fluye a través del circuito se da como
I = VTH/ZTH + ZL
Donde ZL = RL + jXL
ZTH = RTH + jXTH
Por lo tanto, I = VTH/(RL + jXL + RTH + jXTH)
= VTH/((RL + RTH) + j (XL + XTH))
La potencia entregada a la carga,
PL = I2 RL
PL = V2TH × RL/((RL + RTH) 2 + (XL + XTH) ) 2) … … (1)
Para la potencia máxima, la derivada de la ecuación anterior debe ser cero, después de la simplificación obtenemos
XL + XTH = 0
XL =-XTH
Poniendo la relación anterior en la ecuación 1, obtenemos
PL = V2TH × RL/((RL + RTH) 2
De nuevo para la máxima transferencia de potencia, la derivación de la ecuación anterior debe ser igual a cero, después de la simplificación obtenemos
RL + RTH = 2 RL
RL = RTH
Por lo tanto, la potencia máxima se transferirá a la carga desde la fuente, si RL = RTH y XL =-XTH en una Circuito de CA. Esto significa que la impedancia de carga debe ser igual al complejo conjugado de la impedancia equivalente del circuito,
ZL = ZTH
Donde ZTH es el conjugado complejo de la impedancia equivalente del circuito.
Esta potencia máxima transferida, Pmax = V2TH/4 RTH o V2TH/4 RL
Aplicación del ejemplo de transferencia máxima de potencia al circuito de CC
Considere el siguiente circuito para el cual determinamos el valor de la resistencia de carga que recibe t La potencia máxima de la fuente de suministro y la potencia máxima bajo la condición de transferencia de potencia máxima.
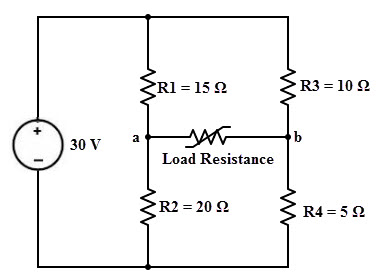
1.Desconecte la resistencia de carga de los terminales de carga a y b. Para representar el circuito dado como el equivalente de Thevenin, debemos determinar el voltaje de Thevenin VTH y la resistencia equivalente de Thevenin RTH.
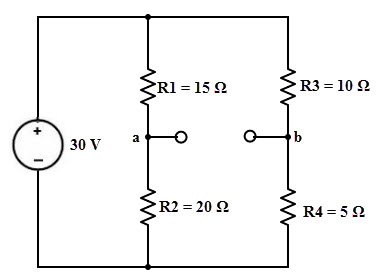
The Thevenin ’ s voltaje o voltaje en los terminales ab es Vab = Va-Vb
Va = V × R2/(R1 + R2)
= 30 × 20/× (20 + 15)
= 17.14 V
Vb = V × R4/(R3 + R4)
= 30 × 5/(10 + 5)
= 10 V
Vab = 17.14-10
= 7.14 V
VTH = Vab = 7.14 voltios
2. Calcule la resistencia equivalente de Thevenin RTH reemplazando las fuentes con sus resistencias internas (aquí suponga que la fuente de voltaje tiene resistencia interna cero por lo que se convierte en un corto en circuito).
La resistencia o resistencia equivalente de Thevenin en los terminales ab es
RTH = Rab = [R1R2/(R1 + R2)] + [R3R4/(R3 + R4)]
= [(15 × 20)/(15 + 20)] + [(10 × 5)/( 10+ 5)]
= 8.57 + 3.33
RTH = 11.90 Ohms
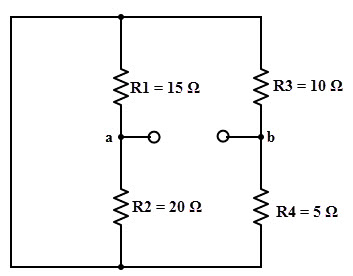
3. El circuito equivalente de Thevenin con los valores calculados anteriormente volviendo a conectar la resistencia de carga se muestra a continuación.
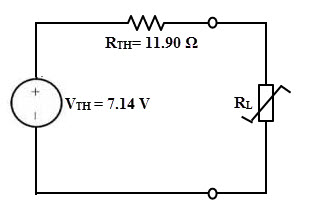
A partir del teorema de transferencia máxima de potencia, el valor de RL debe ser igual al RTH para entregar la potencia máxima a la carga.
Por lo tanto, RL = RTH = 11.90 Ohms
Y la potencia máxima transferida bajo esta condición es,
Pmax = V2TH/4 RTH
= (7.14) 2/(4 × 11.90)
= 50.97/47.6
= 1.07 vatios
Aplicación de la transferencia de energía máxima al circuito de CA
La siguiente red de CA consiste en una impedancia de carga ZL de qué partes reactivas y resistivas se pueden variar. Por lo tanto, tenemos que determinar el valor de la impedancia de carga a la cual la potencia máxima entregada desde la fuente y el valor de la potencia máxima.
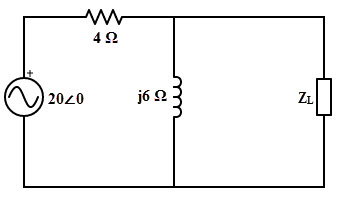
Para encontrar el valor de la impedancia de carga, primero, encontramos el equivalente de Thevenin circuito a través de los terminales de carga. Para encontrar el voltaje de Thevenin, desconecte la impedancia de carga como se muestra en la figura a continuación.
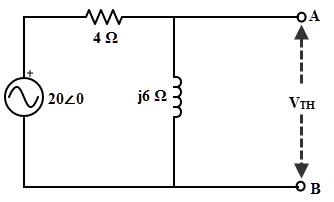
Por regla de divisor de voltaje, VTH = 20∠0 × [j6/(4 + j6)]
= 20∠0 × [6∠90/7.21∠56.3]
= 20∠0 × 0.825∠33.7
VTH = 16.5∠33.7 V
Al acortar la fuente de tensión, calculamos la impedancia equivalente de Thevenin del circuito como se muestra en la figura.
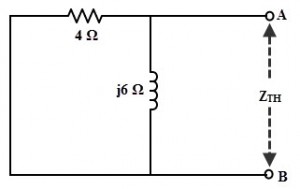
Por lo tanto, ZTH = (4 × j6)/(4 + j6)
= (4 × 6∠90)/(7.21∠56.3)
= 3.33∠33.7 0r 2.77 + j1.85 Ohms
Por lo tanto, el circuito equivalente de Thevenin a través de los terminales de carga se muestra a continuación.
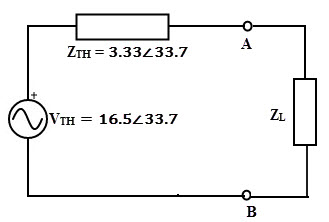
Por lo tanto, para transferir la potencia máxima a la carga, el valor de la impedancia de carga debe ser
ZL = Z × TH
= 2.77-j1.85 ohms
= 2.77-j1.85 ohms
La potencia máxima entregada, Pmax
= V2TH/4 RTH
= (16.5) 2/4 (2.77 )
= 272.25/11.08
= 24.5 W
Aplicación práctica del teorema de máxima transferencia de energía
Considere el ejemplo práctico de un altavoz con una impedancia de 8 ohmios que funciona con audio amplificador con su impedancia interna de 500 ohmios. El circuito equivalente de Thevenin también se muestra en la figura.
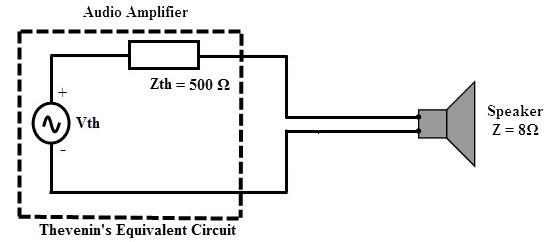
Según el teorema de transferencia máxima de potencia, la potencia se maximiza con la carga si la impedancia de carga es de 500 ohmios (igual que la impedancia interna) ) O bien, la resistencia interna debe cambiarse a 8 ohm para lograr la condición, pero no es posible. Por lo tanto, es una condición de desajuste de impedancia y se puede superar utilizando un transformador de adaptación de impedancia con una relación de transformación de impedancia de 500: 8.