Se dice que los inductores están conectados en paralelo cuando dos terminales de un inductor respectivamente están conectados a cada terminal de otros inductores o inductor. De forma similar a la conexión en paralelo de resistencias, la inductancia total en conexión paralela de inductores es algo menor que la inductancia más pequeña de un inductor en esa conexión.
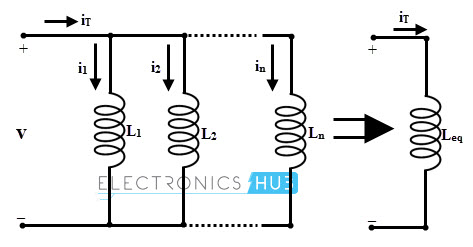
Cuando los inductores están conectados en paralelo, el flujo de corriente a través de cada inductor no es exactamente igual a la corriente total, pero la suma de cada corriente individual a través de inductores paralelos da la corriente total (ya que se divide entre inductores paralelos ).
Si el flujo de corriente a través de cada inductor es menor que la corriente total, el campo magnético generado por cada inductor también es menor que el del campo generado por la corriente total a través de él.
En caso de resistencias en paralelo, la mayor parte de la corriente fluye a través de stor ya que ofrece la menor oposición al flujo de corriente que la resistencia más grande.
Del mismo modo, si los inductores están conectados en paralelo, la corriente elige menos camino de oposición del inductor cuando la corriente en ese circuito disminuye o aumenta mientras inductor se opone individualmente a ese cambio (aumento o disminución de la corriente).
En la conexión en paralelo, el voltaje en cada inductor es igual y también si se cambia la corriente total, la caída de voltaje en cada inductor individual será menor en comparación con la conexión en serie. Para una tasa dada de cambio de corriente, menos será la inductancia en menos voltaje.
Estos son los puntos básicos a considerar en la conexión en paralelo de los inductores. Ahora discutiremos la conexión en paralelo de inductores con y sin considerar el acoplamiento mutuo entre estos inductores.
Índice
- Inductores conectados en paralelo (sin acoplamiento magnético)
- Ejemplo de inductores conectados en paralelo
- Inductores mutuamente acoplados en paralelo
- Inductores de ayuda paralela
- Inductores de ayuda en paralelo Ejemplo
- Inductores opuestos paralelos
- Inductores opuestos en paralelo Ejemplo
- Resumen
Inductores conectados en paralelo (sin acoplamiento magnético)
Como mencionamos anteriormente, un extremo de inductores está conectado a un nodo y a otros extremos de inductores están colectivamente conectados a otro nodo en conexión en paralelo. La conexión paralela de n inductores se muestra en la figura siguiente.
Considere que no hay acoplamiento magnético entre inductores y, por lo tanto, la inductancia total es igual a la suma de recíprocos de las inductancias individuales. Vamos a discutir cómo se puede obtener esta declaración.
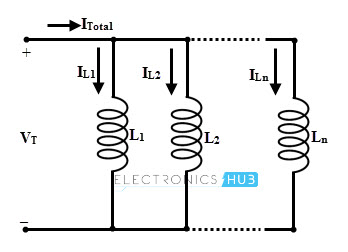
Sabemos que, en una red paralela, el voltaje permanece constante y la corriente se divide en cada inductor paralelo. Si IL1, IL2, IL3 y así sucesivamente ILn son las corrientes individuales que fluyen en los inductores conectados en paralelo L1, L2 y así sucesivamente Ln, respectivamente, entonces la corriente total en los inductores paralelos está dada por
ITotal = IL1 + IL2 + IL3…. + En
Si la tensión individual cae en la conexión paralela son VL1, VL2, VL3 y así sucesivamente VLn, entonces la caída total de tensión entre los dos terminales VT es
VTotal = VL1 = VL2 = VL3…. = Vn
La caída de tensión en términos de auto inductancia se puede expresar como V = L di/dt. Esto implica una caída de voltaje total,
VT = LT di/dt
⇒ LT d/dt (IL1 + IL2 + IL3…. + In)
⇒ LT ((di1)/dt + (di2)/dt + (di3)/dt..)
Sustituyendo V/L en lugar de di/dt, la ecuación anterior se convierte en
VT = LT (V/L1 + V/L2 + V/L3…)
Como la caída de voltaje es constante en todo el circuito, entonces v = VT. Entonces podemos escribir
1/LT = 1/L1 + 1/L2 + 1/L3…..
Esto significa que el recíproco de la inductancia total de la conexión paralela es la suma de recíprocos de las inductancias individuales de todos los inductores. La ecuación anterior es verdadera cuando no hay mutua inductancia entre las bobinas conectadas en paralelo.
Para evitar la complejidad en el tratamiento de fracciones, podemos usar el método de producto sobre suma para calcular la inductancia total. Si dos inductores están conectados en paralelo, y si no hay inductancia mutua entre ellos, entonces la inductancia total se da como
LT = (L1 × L2)/(L1 + L2)
Ejemplo de Inductores Conectados en Paralelo
Si un circuito tiene 2 inductores de 20 Henry y 30 Henry conectados en paralelo, ¿cuál será la inductancia total de la disposición paralela?
Sol: Sabemos que la fórmula para la inductancia total de la serie, 1/LT = 1/L1 + 1/L2
Dado que L1 = 20 Henry
L2 = 30 Henry
LT = (L1 * L2)/(L11 + L2) = (( 20 * 30))/((20 + 30)) = 600/50 = 12
La inductancia total es LTotal = 12 Henry.
Inductores acoplados mutuamente en paralelo
Cuando existe acoplamiento magnético entre los inductores, la fórmula derivada anterior para la inductancia total debe modificarse porque la inductancia total puede ser más o menos dependiendo del imán direcciones de campo ic de cada inductor. El flujo magnético producido por los inductores conectados en paralelo se conectará entre sí.
Cuando los flujos producidos se encuentran en la misma dirección de flujo magnético, la inductancia mutua aumentará; estas bobinas se llaman bobinas de «ayuda». Si el flujo está en dirección opuesta al flujo magnético, la inductancia mutua disminuirá; estas bobinas se llaman bobinas «opuestas». Esta inductancia mutua dependerá de la distancia colocada entre dos bobinas.
Considere que dos inductores están conectados en paralelo con autoinductancias L1 y L2, y que están mutuamente acoplados con inductancia mutua M como se muestra en la figura siguiente.
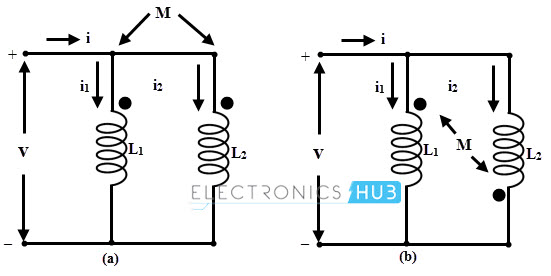
Inductores que ayudan en paralelo
Considere la figura (a), en la cual los inductores L1 y L2 están conectados en paralelo con sus campos magnéticos que ayudan. La corriente total a través del circuito se da como
i = i1 + i2
di/dt = (di1)/dt + (di2)/dt…………. (1)
El voltaje en el inductor o en la rama paralela se da como
V = L1 (di1)/dt + M (di2)/dt o L2 (di2)/dt + M (di1)/dt
L1 (di1)/dt + M (di2)/dt = L2 (di2)/dt + M (di1)/dt
(di1)/dt (L1-M) = ( di2)/dt (L2-M)
(di1)/dt = (di2)/dt ((L2-M))/((L1-M ))…………. (2)
Sustituyendo la ecuación 2 en la ecuación 1, obtenemos
di/dt = (di2)/dt ((L2-M))/((L1-M)) + (di2)/dt
di/dt = (di2)/dt {(L2-M))/((L1-M)) + 1…………. (3)
Si LT es la inductancia total del circuito inductor paralelo, entonces el voltaje viene dado por
V = LT di/dt
LT di/dt = L1 (di1)/dt + M (di2)/dt
di/dt = 1/LT {L1 (di1)/dt + M (di2)/dt
Sustituyendo la ecuación 2 en la ecuación anterior, obtenemos
di/dt = 1/LT {L1 (di2)/dt (L2-M))/(L1-M)) + M (di2)/dt
di/dt = 1/LT {L1 (L2-M))/((L1-M) ) + M (di2)/dt…………. (4)
Igualando las ecuaciones 3 y 4 obtenemos
(L2-M))/((L1-M)) + 1 = 1/LT {L1 (L2-M))/((L1-M)) + M
Simplificando la ecuación anterior, resultados
LT = (L1 L2-M2)/(L1 + L1)-2M)
Aquí 2M representa el flujo magnético de L1 en L2 o L2 en L1. Si la magnitud de dos inductancias es igual a un acoplamiento magnético perfecto entre ellas, la inductancia equivalente de dos inductores es L porque LT = L1 = L2 = M. En tal caso, si la inductancia mutua es cero, la inductancia total sería L ÷ 2.
Ejemplo de Inductores de Ayuda Paralela
Si los dos inductores 25mH y 45mH están conectados en ayuda paralela, calcule la inductancia total de la combinación en paralelo. La inductancia mutua se da como 20mH.
SolGiven, L1 = 25 mH
L2 = 45 mH
M = 20 mH
Aplicando la fórmula para la inductancia total de los inductores auxiliares, LT = (L1 L2-M2 )/(L1 + L1)-2M)
LT = (25 * 45-202)/(25 + 45-2 * 20)
= (1125-400)/(70-40)
= 725/30
= 24.166mH
Por lo tanto, la inductancia total es 24.166 milli Henry.
Inductores opuestos paralelos
De manera similar, si consideramos la figura (b), en qué inductores L1 y amp; L2 están conectados en paralelo con sus campos magnéticos opuestos, la inductancia total se da como
LT = (L1 L2-M2)/(L1 + L2) + 2M)
En inductores paralelos opuestos, si las magnitudes de dos inductancias son iguales con el acoplamiento magnético perfecto, la inductancia equivalente de dos inductores será cero, ya que se anulan entre sí. Si dos inductores permiten efectivamente que la corriente fluya a través de ellos, la inductancia total se da como (L ± M) ÷2.
Inductores opuestos paralelos Ejemplo
Ej.: Si los dos inductores 25mH y 45mH están conectados en paralelo oponiéndose, calcule la inductancia total de la combinación paralela. La inductancia mutua se da como 20mH.
Sol: dado que, L1 = 25 mH
L2 = 45 mH
M = 20 mH
Aplicando la fórmula para la inductancia total de los inductores auxiliares, LT = (L1 L2 M2)/(L1 + L2) + 2M)
LT = (25 * 45-202)/(25 + 45 + 2 * 20)
= (1125-400)/(70 + 40)
= 725/110
= 6.59mH
Por lo tanto, la inductancia total es 6.59 milli Henry.
Resumen
- Conectando los dos terminales del inductor respectivamente a otros terminales de inductor o inductores, entonces esa conexión se conoce como «conexión en paralelo de inductores».
- Cuando los flujos producidos por inductores individuales son en la misma dirección, la inductancia mutua aumentará; luego estas bobinas se llaman bobinas de «Ayuda». La inductancia total para ayudar a las bobinas es LT = (L1 L2-M2)/(L1 + L2)-2M). Cuando los flujos producidos por inductores individuales están en la dirección opuesta al flujo magnético, la inductancia mutua disminuirá; entonces estas bobinas se llaman bobinas «opuestas». La inductancia total para ayudar a las bobinas es LT = (L1 L2-M2)/(L1 + L2) + 2M)