Resistencias en serie y en paralelo
Las resistencias se pueden conectar en serie solo o solo en paralelo. Algunos circuitos de resistencias están hechos de una combinación de redes en serie y paralelas para desarrollar circuitos más complejos. Estos circuitos se conocen generalmente como Circuitos de Resistencia Mixta. Aunque estos circuitos tienen circuitos combinados en serie y en paralelo, no hay cambio en el método de cálculo de la resistencia equivalente. Las reglas básicas de redes individuales como «los mismos flujos de corriente a través de resistencias en serie» y «voltaje entre resistencias en paralelo es el mismo» son aplicables a circuitos mixtos.
A continuación, se muestra un ejemplo de circuito de resistencias mixtas
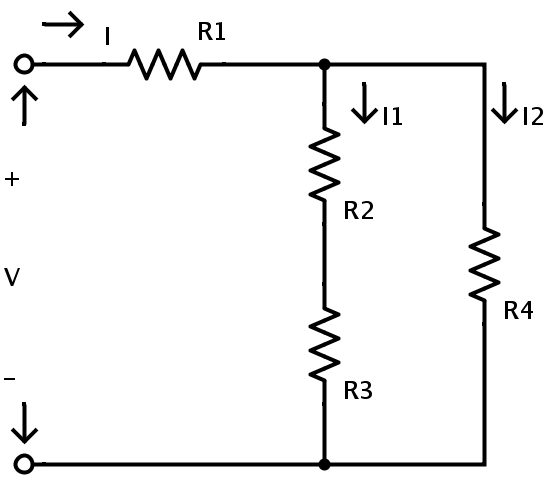
Consiste en cuatro resistencias R1, R2, R3 y R4 en una combinación de circuito de resistencia mixta. La tensión de alimentación es V y la corriente total que fluye en el circuito es I. La corriente que fluye a través de las resistencias R2 y R3 es I1 y la corriente que fluye a través de la resistencia R4 es I2.
Aquí las resistencias R2 y R3 están en combinación de serie. Por lo tanto, al aplicar la regla de resistencias en combinación en serie, la resistencia equivalente de R2 y R3 se da como
RA = R2 + R3
Aquí RA es la resistencia equivalente de R2 y R3
Ahora las resistencias R2 y R3 pueden ser reemplazadas por una sola resistencia RA. El circuito resultante se muestra a continuación.
Ahora las resistencias RA y R4 están en combinación en paralelo. Por lo tanto, al aplicar la regla de resistencias en combinación paralela, la resistencia equivalente de RA y R4 es
RB = RA × R4/(RA + R4)
Aquí RB es la resistencia equivalente de RA y R4
Ahora podemos reemplazar las resistencias RA y R4 con una sola resistencia RB.Después de reemplazar las resistencias, se muestra el circuito resultante a continuación.
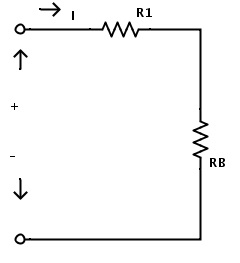
Ahora el circuito consta de solo dos resistencias. Aquí también las resistencias R1 y RB están en combinación en serie. Por lo tanto, aplicando la regla de las resistencias en serie, la resistencia equivalente total del circuito se da como
REQ = R1 + RB
Aquí REQ es la Resistencia equivalente total del circuito. Ahora las resistencias R1 y RB pueden reemplazarse por una sola resistencia REQ.
El circuito equivalente final para el circuito complejo anterior se muestra a continuación.
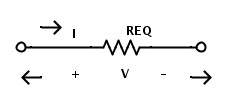
Aunque parezcan complicados, los circuitos de resistencia mixta se pueden reducir a un circuito simple que consiste en una sola fuente de voltaje y una sola resistencia siguiendo las reglas simples de resistencias en serie y resistencias en paralelo.
Resistencias en serie y en paralelo Ejemplo
Calculemos la resistencia equivalente para el circuito inferior que consta de 7 resistencias R1 = 4 Ω, R2 = 4 Ω, R3 = 8 Ω, R4 = 10 Ω, R5 = 4Ω, R6 = 2 Ω y R7 = 2Ω. La tensión de alimentación es de 5 V.
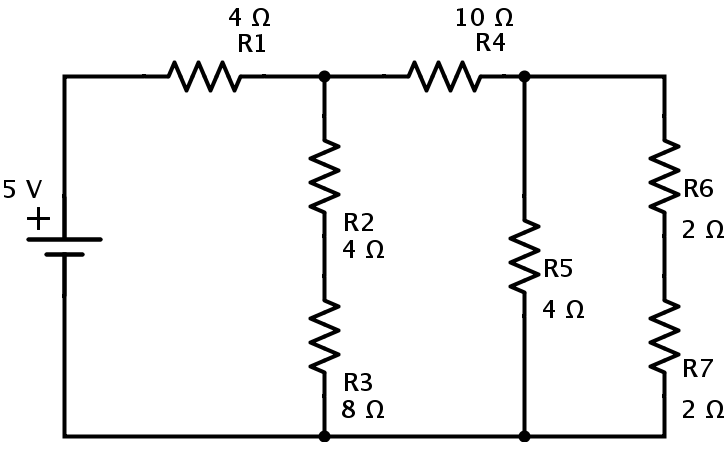
Ahora el resisto rs R6 y R7 están en combinación en serie. Si la resistencia equivalente de las series R6 y R7in es Ra, entonces
Ra = R6 + R7 = 2 + 2 = 4Ω
El resultado el circuito se reduce al que se muestra a continuación.
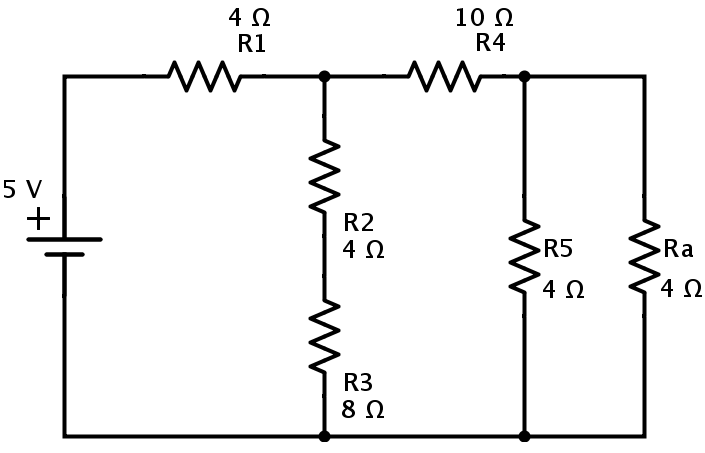
En el circuito anterior, las resistencias Ra y R5 están en combinación en paralelo. Por lo tanto, la resistencia equivalente de Ra y R5 es
Rb = (Ra × R5)/(Ra + R5) = (4 × 4)/(4 + 4 ) = 2Ω.
Luego se muestra el circuito simplificado.
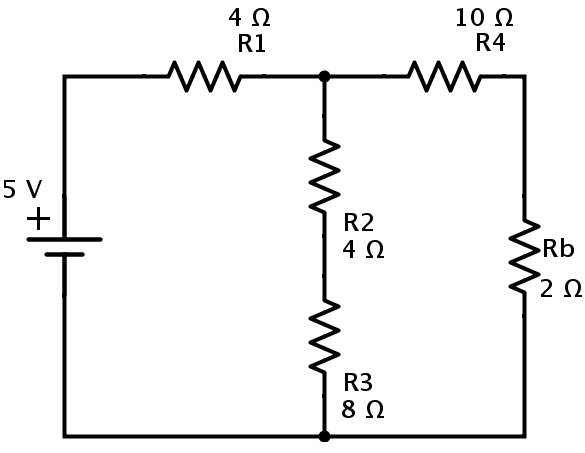
En este circuito, las resistencias R4 y Rb son en combinación de series.
Rc = R4 + Rb = 10 + 2 = 12 Ω.
Ahora podemos reemplazar las resistencias R4 y Rb con la resistencia Rc como se muestra a continuación.
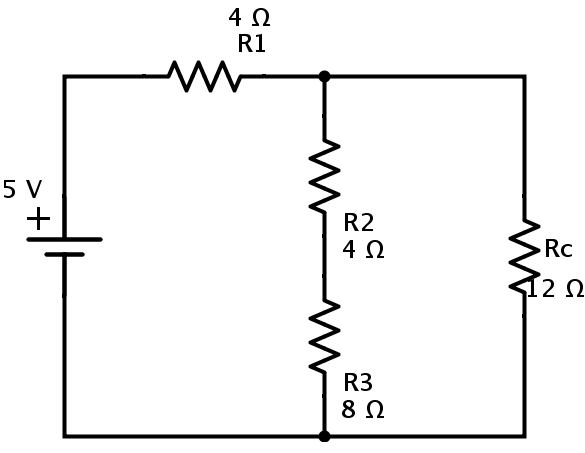
En el circuito de arriba, las resistencias R2 y R3 están en combinación en serie. Si Rd es la resistencia equivalente de R2 y R3, entonces
Rd = R2 + R3 = 4 + 8 = 12 Ω.
El circuito equivalente es
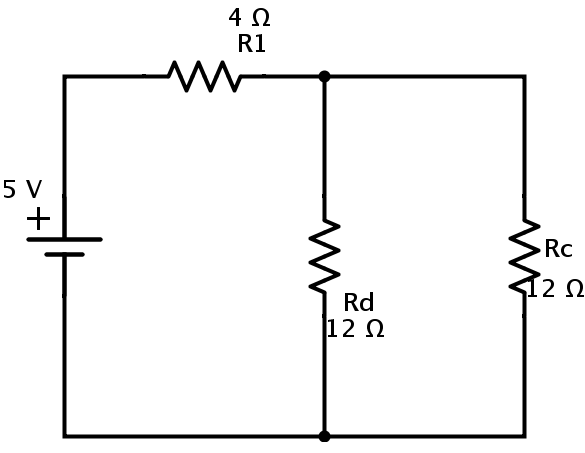
Aquí las resistencias Rc y Rd están en combinación en paralelo. Deje Rp ser la resistencia equivalente de Rc y Rd en paralelo. Entonces
Rp = (Rc × Rd)/(Rc + Rd) = (12 × 12)/(12 + 12) = 6 Ω.
El circuito resultante es
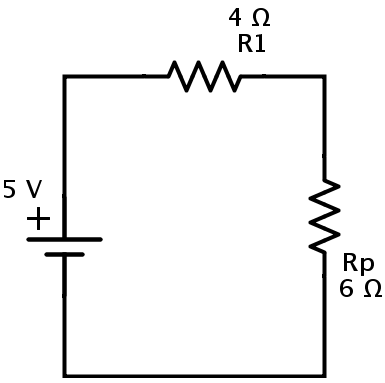
Aquí, las resistencias R1 y Rp están en combinación en serie. Deje que REQ sea la resistencia equivalente de esta combinación.
Luego
REQ = R1 + Rp = 4 + 6 = 10 Ω.
Esta es la resistencia equivalente del circuito. Por lo tanto, el circuito dado se puede volver a dibujar como
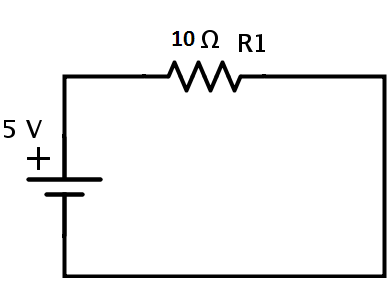
La corriente en el circuito puede calcularse a partir del estilo de la ley de Ohm
I = V/REQ = 5/10 = 0.5 A
Red de resistencias
Calculemos la resistencia equivalente para un circuito de resistencia complejo.
El siguiente circuito consta de diez resistencias R1 a R10 conectadas en una combinación de conexiones en serie y paralelas.
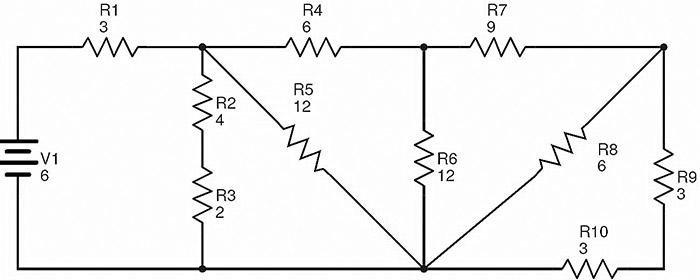
Los valores del las resistencias mencionadas en el circuito están en ohmios (Ω) y la tensión de alimentación está en voltios (V).
Aquí las resistencias R9 y R10 están en combinación en serie. Deje RA es la resistencia equivalente de esta combinación.
Por lo tanto RA = R9 + R10 = 3 + 3 = 6 Ω.
El circuito después de reemplazar R9 y R10 con RA es
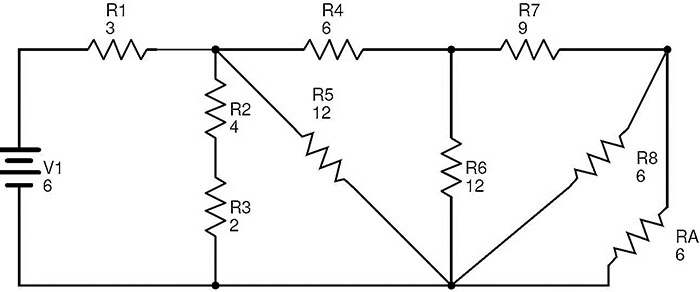
En este circuito, las resistencias R8 y RA están en combinación en paralelo. Entonces la resistencia equivalente de R8 y RA es
RB = (R8 × RA)/(R8 + RA) = (6 × 6)/(6 + 6 ) = 3 Ω.
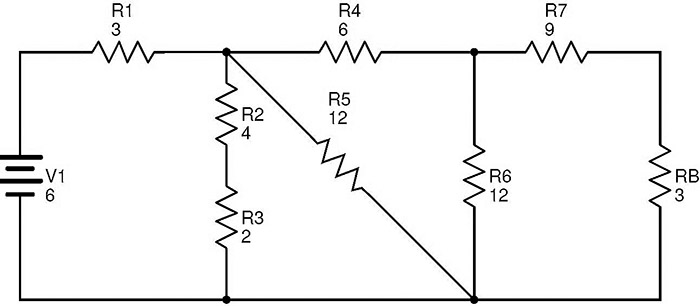
Ahora reemplazando R8 y RA con RB, obtenemos el siguiente circuito.
& nbsp;
En este circuito, las resistencias R7 y RB están en combinación en serie.
RC = R7 + RB = 9 + 3 = 12 Ω.
El circuito equivalente después de reemplazar R7 y RB con RC es
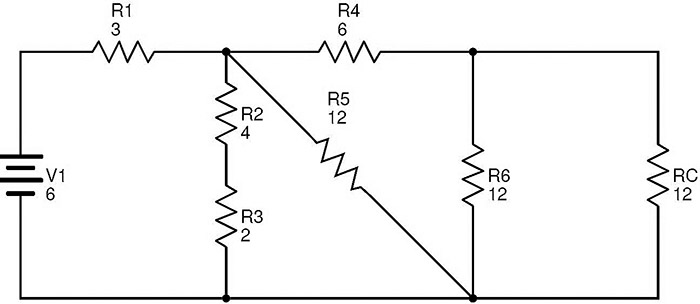
Está claro que las resistencias R6 y Rc están en combinación en paralelo. Si RD es la resistencia equivalente de esta combinación, entonces
RD = (R6 × Rc)/(R6 + Rc) = (12 × 12)/(12 + 12) = 6 Ω.
El circuito con R¬D reemplazando a R6 y Rc es
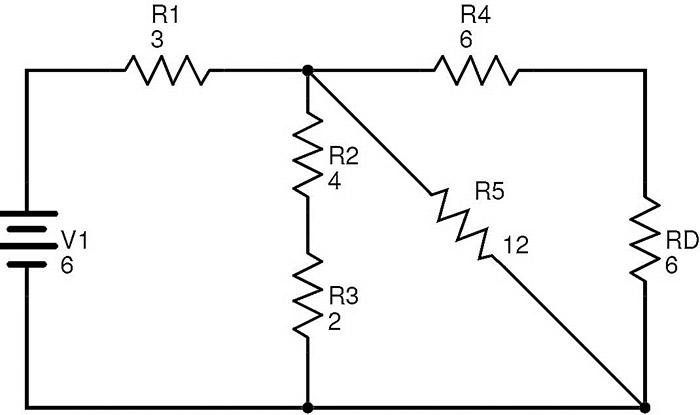
Ahora las resistencias R4 y RD están en combinación de serie. Si RE es la resistencia equivalente de R4 y RD, entonces
RE = R4 + RD = 6 + 6 = 12 Ω.
El resultado circuito reducido después de reemplazar R4 y RD con RE es
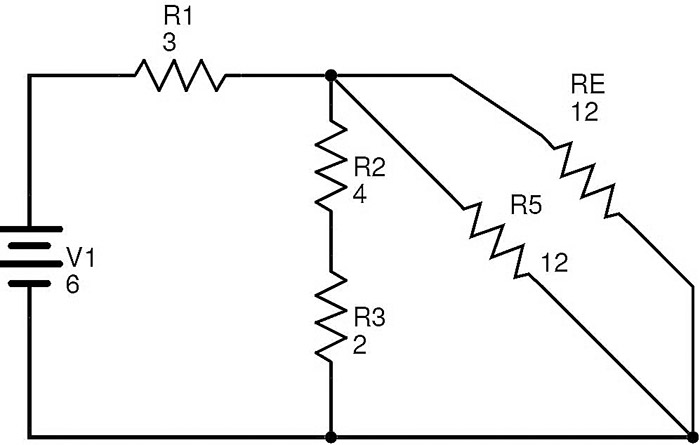
En este circuito, las resistencias R5 y RE están en combinación paralela.
Deje que RF sea la resistencia equivalente de R5 y RE en paralelo.
Luego
RF = (R5 × RE)/(R5 + RE ) = (12 × 12)/(12 + 12) = 6 Ω.
El circuito simplificado es el que se muestra a continuación.
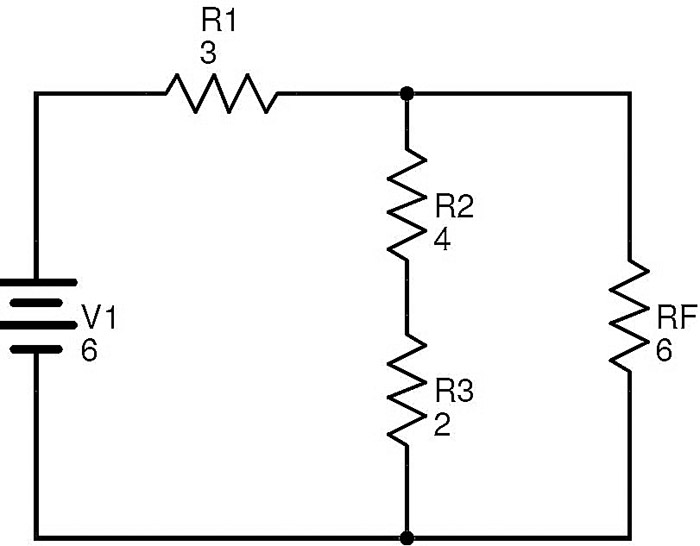
Aquí las resistencias R2 y R3 están en serie. Si RG es el equivalente de esta combinación, entonces
RG = R2 + R3 = 4 + 2 = 6 Ω.
Después de reemplazar a R2 y R3 con RG, el circuito se transformará en
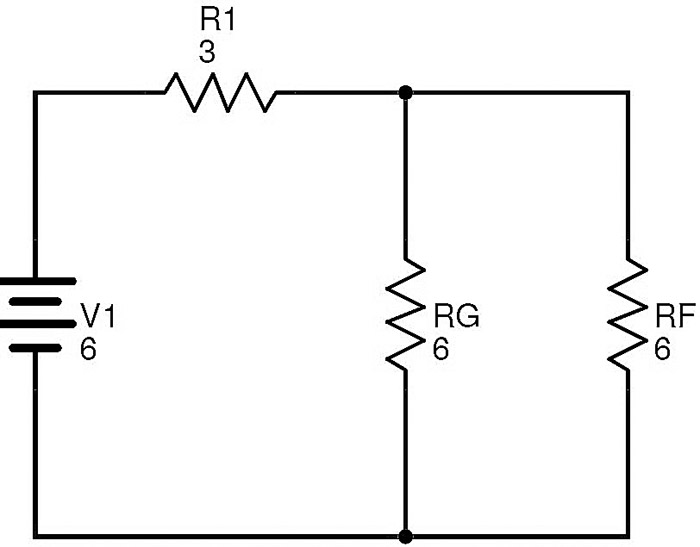
Las resistencias RF y RG están en paralelo.
Deje RT ser el equivalente de esta combinación.
Then RT = (RF × RG)/(RF + RG) = (6 × 6)/(6 + 6) = 3 Ω.
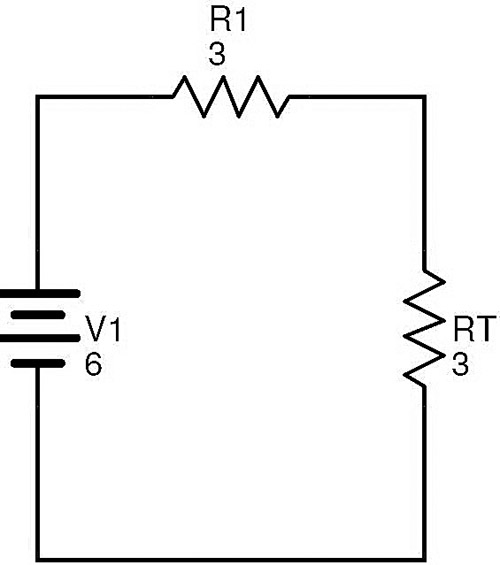
Ahora las resistencias R1 y RT están en serie. Si REQ es la resistencia equivalente del circuito total, entonces REQ = R1 + RT = 3 + 3 = 6 Ω.
Finalmente, el circuito complejo anterior puede redibujarse de la siguiente manera
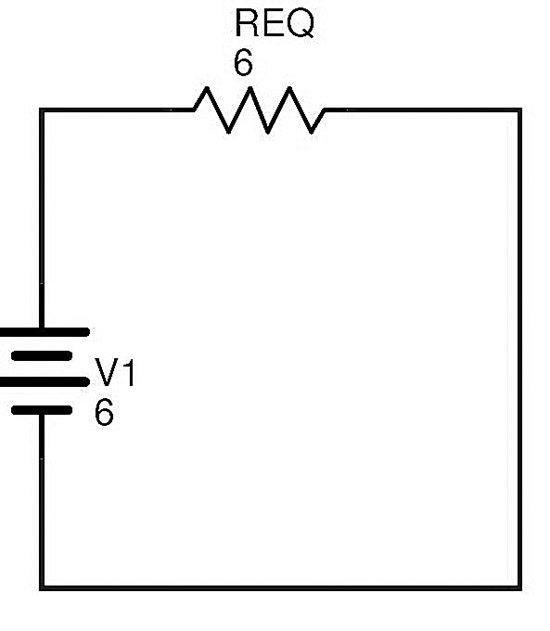
La corriente total en el circuito puede calcularse usando la ley de Ohm
I = V1/REQ = 6/6 = 1 A
Por lo tanto, cualquier circuito resistivo complejo que consista en un número de resistencias conectadas en combinación de combinaciones tanto en serie como paralelas se puede reducir identificando primero las bifurcaciones de resistencia paralelas simples y las bifurcaciones de resistencias en serie. La resistencia equivalente de estas ramas simples se calcula y las ramas se reemplazan con la resistencia equivalente. Este proceso reduce la complejidad del circuito. Al continuar este proceso podemos reemplazar un circuito resistivo complejo con una sola resistencia.
Existen algunos circuitos resistivos complejos que no se pueden reducir a circuitos simples simplemente aplicando las reglas de combinaciones resistivas en serie y combinaciones resistivas paralelas. Circuitos como atenuadores T-Pad y algunas redes complejas de puentes resistivos son ejemplos de tales circuitos resistivos complejos. Para simplificar estos complejos circuitos resistivos, se debe seguir un enfoque diferente.
Algunos circuitos resistivos complejos se pueden reducir usando la Ley actual de Kirchhoff y la Ley de voltaje de Kirchhoff.
Para encontrar las corrientes y voltajes en un complejo circuito resistivo simplemente usando la ley de Ohm podrían no ser posibles. Para este tipo de circuitos, las Leyes del circuito de Kirchhoff serán útiles.
Las leyes de los Circuitos de Kirchhoff se basan en el concepto de conservación de la corriente y la energía en un circuito. Hay dos leyes del circuito de Kirchhoff. Primero está la Ley actual de Kirchhoff que trata con la corriente en el nodo y la segunda es la Ley de voltaje de Kirchhoff que trata sobre el voltaje en un circuito cerrado.
La ley actual de Kirchhoff establece que «la corriente que ingresa a un nodo es igual a la corriente dejando el nodo porque no tiene otro lugar donde ir y no se pierde ninguna corriente en el nodo. »
En palabras simples, la Ley actual de Kirchhoff establece que la suma de las corrientes que ingresan a un nodo es igual a la suma de corrientes que salen del circuito.
La Ley de Voltaje de Kirchhoff establece que «el voltaje total en un circuito cerrado es igual a la suma de todas las caídas de voltaje en ese circuito».
En palabras simples, La Ley de Voltaje de Kirchhoff establece que la suma algebraica dirigida de voltajes en un circuito cerrado es igual a cero.
Con la ayuda de estas dos leyes, se pueden calcular los valores de las corrientes y voltajes en cualquier circuito complejo.
Todavía podemos tener algunos circuitos resistivos complejos en los que es difícil identificar el equival En la resistencia de ent, en tales situaciones usaremos Star Delta Transformations de resistencias para simplificar las redes de resistencia.