Contenido
Introducción
Se dice que dos resistencias están conectadas en paralelo si ambos terminales de una resistencia están conectados a cada terminal respectivo de otra resistencia. En una red de resistencias paralelas, la corriente puede tomar más de una ruta a diferencia de la red de resistencias en serie, ya que existen múltiples rutas para que la corriente fluya. Por lo tanto, los circuitos de resistencia paralelos son divisores de corriente.
Resistencias en paralelo
Si dos o más resistencias están conectadas en paralelo, entonces la diferencia de potencial en cada resistencia es mismo. Las resistencias en conexión paralela están conectadas a los mismos nodos. Esto se puede identificar por la presencia de más de una ruta para que fluya la corriente. Por ejemplo, el circuito que se muestra a continuación es una conexión en paralelo de resistencias. La diferencia de potencial en la resistencia R1 es la misma que en la resistencia R2, que es igual al potencial de suministro VAB.
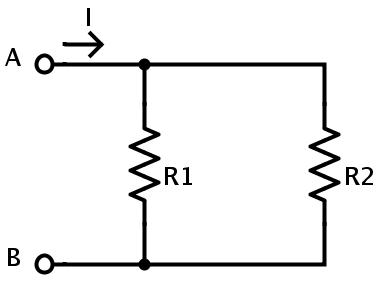
Si VAB es el potencial proporcionado entonces
VR1 = VR2 = VAB
& nbsp;
En el siguiente circuito, las resistencias R1, R2 y R3 están conectadas en combinación paralela.
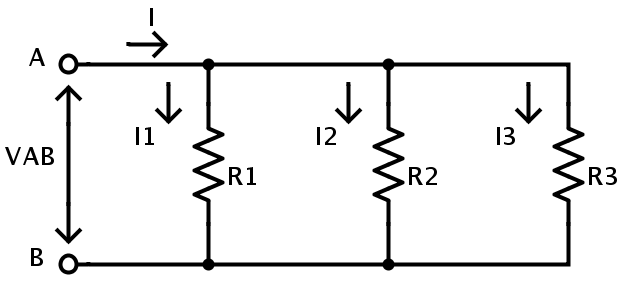
Aquí el potencial de suministro es VAB entre los puntos A y B. Como las resistencias R1, R2 y R3 están conectadas en combinación paralela, la diferencia de potencial en cada resistencia es lo mismo que el suministro. Por lo tanto VAB = VR1 = VR2 = VR3.
Donde
VR1 es el potencial en la resistencia R1.
VR2 es el potencial en la resistencia R2.
VR3 es el potencial en la resistencia R3.
Pero la corriente que fluye a través de estas tres resistencias es diferente. Si I es la corriente que sale del nodo A, entonces tiene tres caminos para llegar al nodo B. La corriente que fluye a través de cada resistencia depende de su resistencia. Por lo tanto, en el caso de circuitos resistivos paralelos, la corriente no es la misma en todas las resistencias. Si I1 es la corriente que fluye a través de la resistencia R1, I2 es la corriente que fluye a través de la resistencia R2 e I3 es la corriente que fluye a través de la resistencia R3, entonces las corrientes I, I1, I2 e I3 pueden relacionarse con la Ley Kirchhoff actual.. De acuerdo con la Ley actual de Kirchhoff, «la suma de las corrientes que ingresan a un nodo es igual a la suma de las corrientes que salen del nodo».
Por lo tanto,
I = I1 + I2 + I3.
Resistencia equivalente Fórmula
Cualquier cantidad de resistencias conectadas en un la combinación en paralelo puede ser reemplazada por una sola resistencia con la resistencia igual a la resistencia equivalente de las resistencias de combinación paralelas.
Se ha establecido que la tensión a través de cada resistencia en una combinación paralela es la misma y la corriente total es igual a la suma de las corrientes individuales. Considere el siguiente circuito.
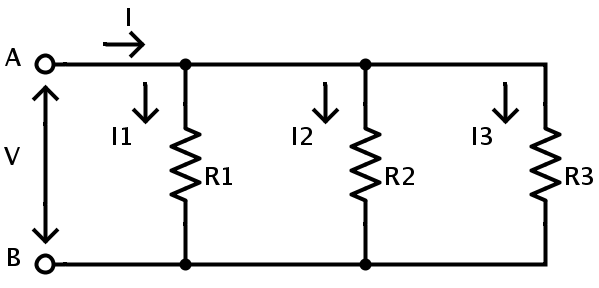
Aquí, I = I1 + I2 + I3
I1 = V/R1
I2 = V/R2
I3 = V/R3
Si RT es la resistencia total del circuito, entonces
I = V/RT
Por lo tanto, V/RT = V/R1 + V/R2 + V/R3
1/RT = 1/R1 + 1/R2 + 1/R3
Si Req es la resistencia equivalente del circuito, se calcula agregando los valores recíprocos de las resistencias individuales (1/R). La inversa de esta suma algebraica dará la resistencia equivalente. La ecuación para la resistencia equivalente Req se muestra a continuación para un circuito resistivo paralelo de n resistencias.
(1/Req) = (1/R1) + (1/R2) + (1/R3) + … … … + (1/Rn)
Se puede hacer una observación a partir de la ecuación anterior de que la resistencia equivalente de las resistencias conectadas en paralelo es siempre menor que la resistencia de la resistencia más pequeña.
Si hay hay dos resistencias en paralelo, entonces la resistencia equivalente es
(1/Req) = (1/R1) + (1/R2)
REQ = R1 * R1/(R1 + R2)
Si dos resistencias de igual resistencia R están conectadas en combinación paralela, entonces la resistencia equivalente de la combinación es R/2.
De manera similar, si tres resistencias de igual resistencia R están conectadas en combinación paralela, entonces la resistencia equivalente de la combinación es R/3.
La conexión en paralelo de las resistencias da la valor de conductancia. La conductancia es el recíproco de la resistencia. En general, está representado por el símbolo G. Las unidades de Conductancia son Siemens representadas por el símbolo S. Anteriormente, las unidades de conductancia son Mho (℧), que es ortografía hacia atrás de Ohm y el símbolo es la representación invertida de Ω.
Aunque las resistencias paralelas están conectadas entre dos nodos, la representación de esta conexión puede tomar cualquiera de las siguientes formas.

Todas las combinaciones mencionadas anteriormente son circuitos resistivos paralelos y todas las reglas de resistencia paralelas también son aplicables a las combinaciones mencionadas anteriormente.
Cálculo actual
La corriente en cada rama de un circuito resistivo paralelo es diferente de la otra. Como el voltaje en cada resistencia es el mismo, la corriente que fluye a través de cada resistencia depende de la resistencia de esa resistencia. Por lo tanto, si el valor de resistencia en una rama es diferente de la otra rama, entonces la corriente en esas ramas será diferente. El valor de esa corriente puede determinarse usando la Ley de Ohm.
Considere una red paralela de dos resistencias con voltaje de suministro V entre dos puntos A y B.

Deje que sea la corriente total en el siguiente circuito.
Deje que la corriente que fluye a través de la resistencia R1 sea IR1 y la corriente fluyendo a través de la resistencia R2 sea IR2.
Luego, de acuerdo con la Ley actual de Kirchhoff, «la corriente total que ingresa a un circuito es igual a la que sale del circuito».
Si TI es el total actual
IT = IR1 + IR2
Como la caída de tensión en cada resistencia es la misma
IR1 = V/R1
E IR2 = V/R2
Si un circuito resistivo paralelo consiste en n resistencias se considera, t cuando la corriente total en el circuito es
ITotal = IR1 + IR2 +…. + IRn
Si los circuitos resistivos en serie se llaman Circuitos Divisores de Voltaje, entonces los circuitos resistivos paralelos se denominan Circuitos Divisores de Corriente.
Si un circuito resistivo paralelo de n resistencias con diferentes resistencias es considerado entonces, es posible tener n rutas diferentes para que la corriente fluya y n valores diferentes de corriente a través de esas rutas. Las resistencias en una combinación en paralelo pueden intercambiarse sin afectar la corriente total y la resistencia equivalente.
Resistencias en el ejemplo paralelo
- Considere el siguiente circuito donde cuatro resistencias R1, R2, R3 y R4 están conectadas en paralelo.
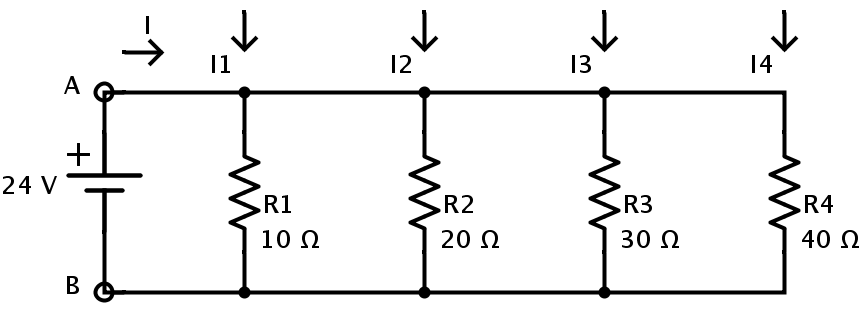
Los valores de resistencia de cada resistencia son
R1 = 10 Ω
R2 = 20 Ω
R3 = 30 Ω
R4 = 40 Ω
La tensión de alimentación es V = 24V
La corriente total en el circuito se puede calcular mediante dos métodos.
El primer método es calcular las corrientes individuales que fluyen a través de cada resistencia.
Si I1 es la corriente que fluye a través de la resistencia R1, entonces de acuerdo con Ley de Ohm
I1 = V/R1 = 24/10 = 2.4 A
De manera similar si I2 es la corriente que fluye a través de la resistencia R2, thena según la ley de Ohm
I2 = V/R2 = 24/20 = 1.2 A
Si I3 es la corriente que fluye a través de la resistencia R3, thena según la ley de Ohm
I3 = V/R3 = 24/30 = 0.8 A
Y si I4 es la corriente que fluye a través del resistencia R4, thena según la ley de Ohm
I4 = V/R4 = 24/40 = 0.6 A
Si ITOTAL es la corriente total en el circuito, luego de acuerdo con la ley actual de Kirchhoff,
ITOTAL = I1 + I2 + I3 + I4 = 2.4 + 1.2 + 0.8 + 0.6 = 5A
El segundo método para calcular la corriente es averiguar la resistencia equivalente del circuito.
La resistencia equivalente del circuito es
1/REQ = (1/R1) + (1/R2) + (1/R3) + (1/R4)
1/REQ = (1/10) + (1/20) + (1/30) + (1/40)
REQ = 1/2.083 = 4.8 Ω
Esta única resistencia se puede usar para reemplazar todas las resistencias en la combinación paralela.
∴ ITOTAL = V/REQ = 24/4.8 = 5A.
Considere el siguiente circuito donde tres resistencias R1, R2 y R3 están conectadas en una combinación paralela.
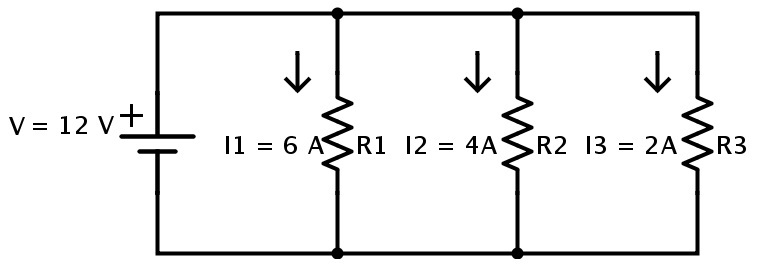
La corriente que fluye a través de R1 es I1 = 6A
La corriente que fluye a través de R2 es I2 = 4A
La corriente que fluye a través de R3 es I3 = 2A
In circuitos resistivos paralelos, la tensión en cada resistencia es la misma y es igual a la tensión de alimentación.
Aquí la tensión de alimentación es V = 12 V.
Si V1 es la tensión en la resistencia R1, V2 es la tensión en la resistencia R2 y V3 es la tensión en la resistencia R3, entonces
V = V1 = V2 = V3 = 12V
Luego según la ley de Ohm
R1 = V1/I1
R1 = 12/6
R1 = 2 Ω
R2 = V2/I2
R2 = 12/4
R2 = 3 Ω
R3 = V3/I3
R3 = 12/2
R3 = 6 Ω
Aplicaciones
El concepto de resistencias en paralelo se usa en el análisis del circuito de puente de Wheatstone. Las resistencias en combinación paralela actúan como circuito divisor de corriente. Este concepto de divisor actual se usa por completo en aplicaciones como convertidores analógico a digital y convertidores digitales a analógicos.