Un inductor es un elemento pasivo que se utiliza en circuitos electrónicos para el almacenamiento temporal de energía eléctrica en forma de flujo magnético o simplemente campo magnético. La inductancia es propiedad de cualquier bobina que pueda configurar el flujo magnético cuando la corriente pase por ella.
Cualquier dispositivo que tenga la propiedad de inductancia se puede llamar inductor. Por lo general, el inductor se construye en forma de una bobina con material de cobre alrededor del núcleo de un medio magnético (hierro) o no magnético (como el aire).
Los inductores pueden conectarse en serie o la configuración en paralelo depende del rendimiento requerido por el circuito. Estas combinaciones se utilizan para diseñar redes más complejas. La inductancia total de un circuito depende de cómo estén conectados los inductores, ya sea en serie o en paralelo.
Además, la manera en que los inductores están conectados de modo que una inductancia no tenga efecto en otros también varía la inductancia total en comparación con el efecto del acoplamiento magnético entre inductores.
Por lo tanto, los inductores se organizan sobre la base de su inductancia mutua o acoplamiento magnético en combinaciones en serie o en paralelo.
Inductores conectados en serie
Supongamos que los inductores conectados en el circuito no tienen ningún acoplamiento entre ellos. Esto implica que no hay líneas de flujo de un inductor que enlace con otro, y por lo tanto no habrá flujo mutuo entre las bobinas.
La conexión de extremo a extremo de dos o más inductores se denomina «conexión en serie de inductores «. A este respecto, los inductores están conectados en serie, por lo que aumentan las vueltas efectivas del inductor. La conexión en serie de los inductores se muestra en el siguiente diagrama
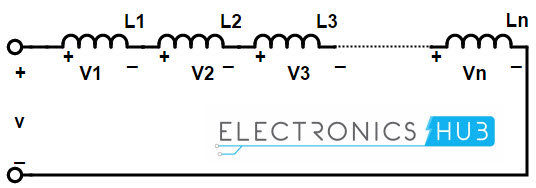
La inductancia de los inductores conectados en serie se calcula como la suma de las inductancias individuales de cada bobina ya que el cambio de corriente a través de cada bobina es mismo.
Esta conexión en serie es similar a la de las resistencias conectadas en serie, excepto que las resistencias son reemplazadas por inductores. Si la corriente I fluye en la conexión en serie y las bobinas son L1, L2, etc., la corriente común en los inductores en serie viene dada por
ITotal = IL1 = IL2 = IL3… = En
Si la tensión individual cae a través de cada bobina en esta conexión en serie son VL1, VL2, V¬L3, y así sucesivamente, la caída total de tensión entre los dos terminales VT está dada por
VTotal = VL1 + VL2 + VL3…. + Vn
Como sabemos que la caída de tensión se puede representar en términos de auto inductancia L, esto implica
V = L di/dt.
Esto también se puede escribir como
LT di/dt = L1 di/dt + L2 di/dt + L3 di/dt +… + Ln di/dt
Por lo tanto, la inductancia total es
LTotal = L1 + L2 + L3 +….. + Ln
Esto significa que la inductancia total de la conexión en serie es la suma de las inductancias individuales de todos los inductores. La ecuación anterior es verdadera cuando no hay efecto de inductancia mutua entre las bobinas en esta configuración de serie.
La inductancia mutua de los inductores hará un cambio en el valor de la inductancia total en la combinación en serie de inductores.
Supongamos que hay dos inductores conectados en serie con la fuente de tensión alterna que puede generar una corriente variable en el circuito como se muestra en la figura anterior.
Si no hay inductancia mutua en el circuito, entonces la inductancia total se da como
LT = L1 + L2
Es importante recordar que la inductancia total es siempre mayor que el inductor más grande en la serie de inductores en serie.
Inductores conectados en serie Ejemplo
Ej 1: Si un circuito tiene 3 inductores de 60 Henry, 30 Henry y 20 Henry conectados en serie, ¿qué será? la inductancia total de la serie?
Sol: sabemos que la fórmula para la inductancia total de la serie, LTotal = L1 + L2 + L3 +….. + Ln
Dado que L1 = 60 Henry
L1 = 30 Henry
L1 = 20 Henry
La inductancia total, LTotal = 60 + 30 + 20 = 110 Henry.
Inductores conectados mutuamente en la serie
Ahora considere que los inductores están conectados de manera que el campo magnético de una bobina afecta al otro. Cuando dos o más inductores están conectados en serie, la inductancia de un inductor se verá afectada por el campo magnético producido por la otra bobina.
Esto se denomina inductancia mutua y las bobinas se denominan «inductores conectados mutuamente». «. Esta inductancia mutua puede aumentar o disminuir la inductancia total del circuito en serie.
El factor que afecta la inductancia mutua de una serie conectada de inductores es la distancia entre las bobinas y su orientación.
Los inductores conectados mutuamente pueden acoplarse en dos tipos
1) Acoplado acumulativo o ayuda en serie
2) Acopladores acoplados o en serie opuestos
Inductores acumulados acumulativamente en la serie
Si los flujos magnéticos producidos por los inductores están en la misma dirección que el flujo de corriente a través de ellos, entonces las bobinas se conocen como «Acopladas acumulativamente».
En esta serie de circuitos acoplados o acumulativos, el la corriente entra o sale de los terminales de las bobinas en cualquier instante de tiempo en la misma dirección.
La figura siguiente muestra la conexión de dos inductores en disposición de ayuda en serie.

Si pasamos la corriente a través de las bobinas acopladas acumulativamente (entre los nodos A y amp; D) en la misma dirección, la caída de tensión de cada bobina individual afectará la inductancia total de la serie.
Permita que la auto inductancia de la bobina-1 sea L1, la auto inductancia de la bobina-2 sea L2 y la inductancia mutua es M entre la bobina 1 y la bobina2.
La fem autoinducida en la bobina-1 es
e1 =-L1 di/dt
La fem inducida mutuamente en la bobina-1 debido al cambio de corriente en la bobina-2 es
eM1 =-M di/dt
Del mismo modo, la fem autoinducida en coil-2 es
e2 =-L2 di/dt
Mutual inducida fem en la bobina-2 debido al cambio de corriente en bobina-1 es
eM2 =-M di/dt
Por lo tanto, fem inducida total en el circuito de ayuda en serie se da como
e =-L1 di/dt-L2 di/dt-2M di/dt
=-(L1 + L2 + 2M) di/dt
Si LT es el total inductancia del circuito, la fem inducida total será equivalente a
e =-LT di/dt
Sustituyendo en la ecuación anterior, obtenemos
-LT di/dt =-(L1 + L2 + 2M) di/dt
Por lo tanto, LT = (L1 + L2 + 2M)
Inductores acoplados acumulativamente en serie Ejemplo
Ej.: si dos bobinas de inductancia 70 mH y 30 mH están conectadas en serie, luego encuentre la inductancia acumulativa total de los inductores conectados en serie. Considere que la inductancia mutua de la combinación de las dos bobinas es de 40 mH.
Sol:
Dado que, L1 = 70 mH
L2 = 30 mH
M = 40 mH
Aplicando la fórmula para inductores conectados de manera acumulativa, LT = L1 + L2 + 2M
LT = 70 + 30 + 2 (40)
= 100 + 80
= 180 mH
Por lo tanto, la inductancia acumulada de la bobina es de 180 mili Henry.
Inductores acoplados diferencialmente en la serie
Si los flujos magnéticos producidos por los inductores están en la dirección opuesta entre sí, entonces el las bobinas se conocen como «acopladas diferencialmente».
En esta conexión de oposición acoplada diferencial o en serie, la corriente entra o sale de los terminales de las bobinas en cualquier instante del tiempo en la dirección opuesta.
La figura a continuación muestra la conexión de dos inductores en disposición de oposición en serie.
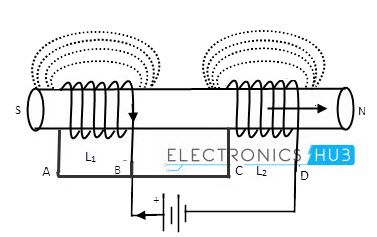
En bobinas acopladas diferencialmente, los campos de flujo magnético pueden producir en la misma dirección o en la dirección opuesta. Deje que la auto inductancia de las bobinas sea L1 y L2 y que la inductancia mutua sea M.
Aquí la inductancia mutua se verá favorecida a cada inductancia de la bobina debido a la configuración del circuito. Por lo tanto, la fem inducida total en el circuito opuesto de la serie se da como
e =-L1 di/dt-L2 di/dt + 2M di/dt
=-(L1 + L2-2M) di/dt
Si LT es la inductancia total del circuito, la fem inducida total será equivalente a
e =-LT di/dt
Sustituyendo en la ecuación anterior, obtenemos
-LT di/dt =-(L1 + L2-2M) di/dt
Por lo tanto, LT = (L1 + L2-2M)
Inductores acoplados diferencialmente en serie Ejemplo
Ej.: si dos bobinas de inductancia 70 mH y 30 mH están conectadas en serie, luego encuentre la inductancia diferencial total de los inductores conectados en serie. Considere que la inductancia mutua de la combinación de las dos bobinas es de 40 mH.
Sol:
Dado que, L1 = 70 mH
L2 = 30 mH
M = 40 mH
Aplicando la fórmula para inductores conectados diferencialmente, LT = L1 + L2-2M
LT = 70 + 30-2 (40)
= 100-80
= 20 mH
Por lo tanto, la inductancia diferencial de la bobina es de 20 mili Henry.
Resumen
- Un inductor es un elemento pasivo que se utiliza en circuitos electrónicos para almacenando energía como flujo magnético. La inductancia se mide en Henry.
- La cantidad de disipación de la potencia real con el flujo de corriente en el circuito se denomina «reactancia inductiva». Se mide en ohms. XL = 2 f L
- La auto inductancia es propiedad de un circuito eléctrico o un circuito en el que su propio campo magnético se opone a cualquier cambio en la corriente
- La inductancia mutua es la capacidad de un inductor que provoca la inducción de fem en otro inductor situado muy cerca de él cuando cambia la corriente en el primer inductor.
- La conexión de extremo a extremo de dos o más inductores se denomina «conexión en serie de inductores». La fórmula para la inductancia total en serie es LT = L1 + L2
- La inductancia total de los inductores conectados en serie es siempre mayor que el inductor más grande en esa serie.
- Si los flujos magnéticos producidos por los inductores están en la misma dirección que el flujo de corriente a través de ellos, entonces las bobinas se conocen como «Acopladas acumulativamente». LT = L1 + L2 + 2M
- Si los flujos magnéticos producidos por los inductores están en la dirección opuesta entre sí, entonces las bobinas se conocen como «acopladas diferencialmente». LT = L1 + L2-2M
muchas gracias por todo.