Contenido
- 1 Introducción
- 2 Circuito activo de filtro de paso bajo
- 3 Filtro de paso bajo activo con ganancia de alta tensión
- 4 Ganancia de voltaje de filtro de paso bajo activa
- 5 Ejemplo de filtro de paso bajo activo:
- 6 Respuesta de frecuencia
- 7 Second Order Active Filtro de paso bajo
- 8 Aplicaciones de filtros activos de paso bajo
Introducción
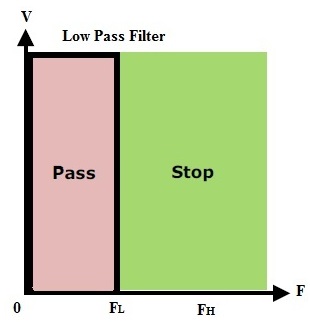
El filtro paso bajo es un filtro que pasa todas las frecuencias desde DC hasta la frecuencia de corte superior fH y rechaza cualquier señal por encima de esta frecuencia.
En el caso ideal, la curva de respuesta de frecuencia cae a la frecuencia de corte. Prácticamente la señal no se reducirá repentinamente, sino que disminuirá gradualmente desde la región de transición a la región de la banda de detención.
Frecuencia de corte significa el punto donde la respuesta cae-3 dB o 70.7% desde la banda de paso. La región de transición significa el área donde ocurre la caída.
La región de parada de la banda significa el área donde la atenuación ocurre principalmente a las señales de entrada. Por lo tanto, este filtro también se conoce como filtro de corte alto o filtro de corte de agudos. La respuesta ideal se muestra a continuación
 En lugar de los componentes pasivos, el filtro activo de paso bajo está formado por componentes activos como op-amperios, FET y transistores. Estos filtros son muy efectivos en comparación con los filtros pasivos. Se introducen filtros activos para superar los defectos de los filtros pasivos.
En lugar de los componentes pasivos, el filtro activo de paso bajo está formado por componentes activos como op-amperios, FET y transistores. Estos filtros son muy efectivos en comparación con los filtros pasivos. Se introducen filtros activos para superar los defectos de los filtros pasivos.
Un filtro de paso bajo activo simple se forma mediante el uso de un amplificador operacional. El amplificador operacional tomará la señal de alta impedancia como entrada y dará una señal de baja impedancia como salida. El componente del amplificador en este circuito de filtro aumentará la amplitud de la señal de salida.
Por esta acción del amplificador, la señal de salida se hará más ancha o más estrecha. La respuesta de frecuencia máxima del filtro depende del amplificador utilizado en el diseño del circuito.
Circuito activo de filtro de paso bajo
La atenuación de la señal que es la amplitud de la señal de salida es menor que la amplitud de la señal de entrada en el circuito pasivo. Para superar esta desventaja del filtro pasivo se diseña un filtro activo. Un filtro pasivo conectado al op-amp inversor o no inversor nos proporciona un filtro de paso bajo activo simple.
El filtro activo de primer orden está formado por un único amplificador operacional con circuito RC. A continuación, se muestra un filtro pasivo RC simple conectado a la terminal no inversora de un amplificador operacional
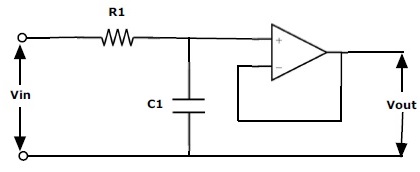
Este circuito RC proporcionará una ruta de baja frecuencia a la entrada del amplificador. El amplificador actúa como un circuito de protección que proporciona salida de ganancia unitaria. Este circuito tiene más valor de impedancia de entrada. Aunque la impedancia de entrada de los amplificadores operacionales es muy alta por debajo de la frecuencia de corte, esta impedancia de entrada está limitada por la impedancia en serie que es igual a R + 1/jωC.
La impedancia de salida de la opción el amplificador que está conectado en el circuito siempre es bajo. Este circuito proporcionará una gran estabilidad al filtro. El principal inconveniente de esta configuración es que la ganancia de voltaje es la unidad. Incluso para este circuito también la potencia de salida es alta ya que la impedancia de entrada es baja.
Filtro de paso bajo activo con ganancia de alta tensión
El circuito de filtro de paso bajo activo anterior no proporciona más que la ganancia de la unidad. Por lo tanto, utilizamos el circuito inferior para proporcionar una ganancia de alto voltaje.
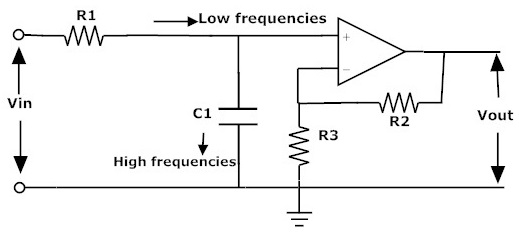
Cuando las señales de entrada están en a bajas frecuencias, las señales pasarán a través del circuito de amplificación directamente, pero si la frecuencia de entrada es alta, las señales pasan a través del condensador C1. Mediante este circuito de filtro la amplitud de la señal de salida aumenta por la ganancia de banda de paso del filtro.
Sabemos que, para el circuito amplificador no inversor, la magnitud de la ganancia de tensión se obtiene por su resistencia de realimentación R2 dividida por su correspondiente resistencia de entrada R3.
Esto se da de la siguiente manera
Magnitud del voltaje Gain = {1 + (R2/R3)
Ganancia de voltaje de filtro de paso bajo activa
Sabemos que la ganancia puede obtenerse por los componentes de frecuencia y esto se da de la siguiente manera
ganancia de voltaje = V_out/V_in = A_max/√ (1+ 〖f/f_c〗 ^ 2)
Donde
- Amax = ganancia de la banda de pase = 1 + R_2/R_3
- f = frecuencia operativa.
- fc = Frecuencia de corte.
- Vout = Voltaje de salida.
- Vin = Voltaje de entrada.
Cuando la frecuencia aumenta, la ganancia disminuye en 20 dB por cada 10 veces que Incremento de frecuencia. Esta operación se observa como se indica a continuación
A bajas frecuencias que es cuando la frecuencia de operación f es menor que la frecuencia de corte, entonces
Vout/Vin = Amax
Cuando la frecuencia de funcionamiento es igual a la frecuencia de corte, entonces
Vout/Vin = Amax/√2 = 0.707 Amax
Cuando la frecuencia de operación es menor que la frecuencia de corte, entonces
Vout/Vin & lt; Amax
Con estas ecuaciones podemos decir que a bajas frecuencias la ganancia del circuito es igual a la ganancia máxima y a altas frecuencias la ganancia del circuito es menor que la ganancia máxima Amax.
Cuando la frecuencia real es igual a la frecuencia de corte, entonces la ganancia es igual al 70.7% del Amax. Con esto podemos decir que por cada aumento de frecuencia de diez veces (década) la ganancia de la tensión se divide por 10.
Magnitud de la ganancia de voltaje (dB): Amax = 20 log10 (Vout/Vin)
A una frecuencia de-3 dB la ganancia se da como:
3 dB Amax = 20 log10 {0.707 (Vout/Vin )
Ejemplo de filtro de paso bajo activo:
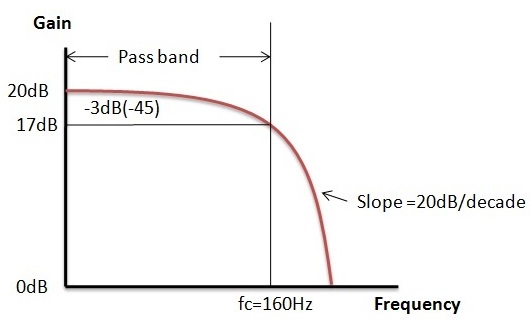
Consideremos un filtro de paso bajo activo no inversor que tiene una frecuencia de corte de 160 Hz y una impedancia de entrada de 15 kΩ. Suponga que a bajas frecuencias este circuito tiene una ganancia de voltaje de 10.
La ganancia en dB se da como 20log (Amax) = 20log (10) = 20 dB
Sabemos que la ganancia de voltaje se da como:
Amax = 10 = 1 + (R2/R1)
Deje que la resistencia R1 sea 1.2 kΩ
R2 = 9R1 = 9 x 1.2k = 10.8 kΩ
Por lo tanto, el R2 obtenido es 10.8 kΩ. Como este valor no existe, podemos considerar el valor estándar preferido más cercano como 11 kΩ.
Al considerar la ecuación de frecuencia de corte, podemos obtener el valor del condensador.
fC = 1/2πRC
Al considerar la C como principal, podemos escribir la ecuación anterior de la siguiente manera
C = 1/2πfCR
Sustituye el valor de la impedancia de entrada como 15 kΩ, valor f_C como 160 Hz.
Por lo tanto, C = 0.068μF.
A partir de los valores obtenidos podemos obtener el filtro de paso bajo activo de la siguiente manera
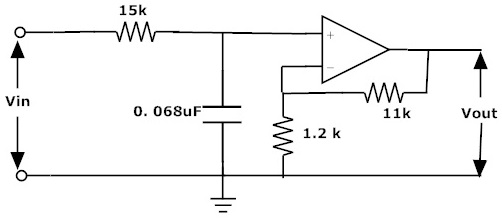
Respuesta de frecuencia
La respuesta del filtro activo es la que se muestra en la figura siguiente
Second Order Active Filtro de paso bajo
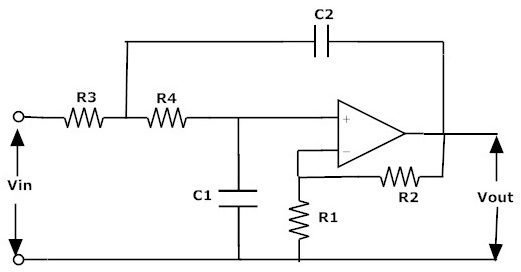
Simplemente agregando un circuito RC adicional al primer orden El filtro de segundo orden se muestra arriba.
La ganancia del circuito anterior es Amax = 1 + ( R2/R1)
La frecuencia de corte del filtro de paso bajo de segundo orden es fc = 1/2π√ (C1C2R3R4)
la respuesta de frecuencia y los pasos de diseño del filtro de segundo orden y el filtro de primer orden son casi los mismos, excepto la caída de la banda de parada. El valor de caída del filtro de segundo orden es el doble que el del filtro de primer orden que es 40dB/década o 12dB/octava. Estos filtros detienen las señales de alta frecuencia más pronunciadas.
Aplicaciones de filtros activos de paso bajo
En electrónica estos filtros son ampliamente utilizados en muchas aplicaciones. Estos filtros se utilizan como filtros de silbido en los parlantes de audio para reducir el silbido de alta frecuencia producido en el sistema y estos se utilizan como entradas para los subwoofers.
Estos también se usan en ecualizadores y amplificadores de audio. En la conversión de analógico a digital, estos se utilizan como filtros anti-aliasing para controlar las señales. En los filtros digitales, estos se utilizan para difuminar imágenes, suavizar conjuntos de señales de datos. En los transmisores de radio para bloquear las emisiones armónicas.
En acústica, estos filtros se utilizan para filtrar las señales de alta frecuencia del sonido de transmisión, lo que provocará eco a frecuencias de sonido más altas.