Circuitos pasivos de filtro de paso bajo de primer orden y segundo orden

 

Introducción

El filtro es un circuito que se usa para filtrar las señales, ya que pasará solo las señales necesarias y evitará señales no deseadas. En general, los filtros están diseñados por componentes pasivos o por componentes activos.

Los componentes pasivos son resistencias, inductores y condensadores.

Los componentes activos son transistores, FET y amplificadores operacionales.

El filtro de paso bajo es un filtro que pasará solo señales de baja frecuencia y atenuará señales de alta frecuencia. Permite señales de solo 0Hz para cortar la frecuencia ‘fc’. Este valor de frecuencia de corte dependerá del valor de los componentes utilizados en el circuito. En general, estos filtros son preferibles por debajo de 100 kHz. La frecuencia de corte también se denomina frecuencia de corte o frecuencia de giro.

Filtro de paso bajo pasivo

El circuito de filtro de paso bajo diseñado por componentes pasivos se conoce como filtro pasivo de paso bajo.

El filtro de paso bajo RC se muestra a continuación

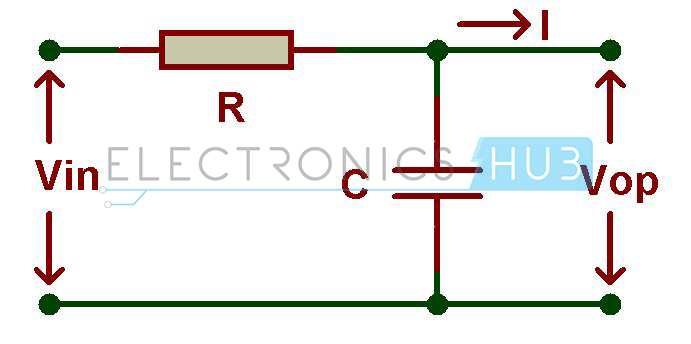
Simplemente conectando la resistencia ‘R’ en serie con un condensador ‘C’ da RC Pass Low Filter. Simplemente puede referirse como filtro de paso bajo (LPF). La resistencia es independiente de las variaciones de las frecuencias aplicadas en el circuito pero el condensador es un componente sensible que significa que responde a los cambios en el circuito.

Dado que tiene solo un componente reactivo, este circuito también se puede denominar como ‘filtro de un polo’ o ‘filtro de primer orden’. La tensión de entrada «Vin» se aplica a todo el ciclo de la serie y la tensión de salida solo se aplica a través del condensador.

Dado que el condensador es un componente sensible, la concentración principal a observar se refiere a la «reactancia capacitiva». La reactancia capacitiva es la respuesta de la oposición creada por el condensador en el circuito.

Para mantener la capacitancia del condensador, el condensador se opondrá a una pequeña cantidad de flujo de corriente en el circuito. Esta oposición al flujo de corriente en el circuito se llama impedancia. Por lo tanto, la reactancia capacitiva disminuye con el aumento de la corriente opuesta.

Con esto podemos decir que la reactancia capacitiva es inversamente proporcional a la frecuencia aplicada al circuito. El valor resistivo de la resistencia es estable mientras que el valor de la reactancia capacitiva varía. La caída de tensión en el condensador es muy inferior en comparación con el potencial de tensión del condensador.

Esto significa que a bajas frecuencias la caída de voltaje es pequeña y el potencial de voltaje es grande, pero a altas frecuencias la caída de voltaje es muy alta y el potencial de voltaje es menor. Por este fenómeno podemos decir que el circuito anterior puede actuar como un circuito ‘divisor de voltaje de frecuencia variable’.

La reactancia capacitiva se puede formular de la siguiente manera:

Cálculo de la tensión de salida

Para obtener la ecuación del divisor potencial, debemos considerar la impedancia, la reactancia capacitiva, el voltaje de entrada y la tensión de salida. Al usar estos términos, podemos formular la ecuación para la ecuación del divisor potencial RC de la siguiente manera

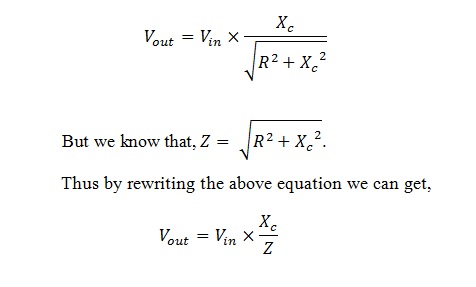Al usar esta ecuación, podemos calcular el valor de la salida en cualquier frecuencia aplicada.

Low Ejemplo de filtro de paso

Examinemos estos valores de voltaje de salida y los valores de reactancia capacitiva considerando los valores de resistencia y capacitor. Deje que el valor de la resistencia R sea de 4.7kΩ y el valor del condensador como 47nF. La entrada de voltaje A.C suministrada es de 10V. Los valores de frecuencia para los que vamos a calcular son de 1 kHz y 10 kHz.

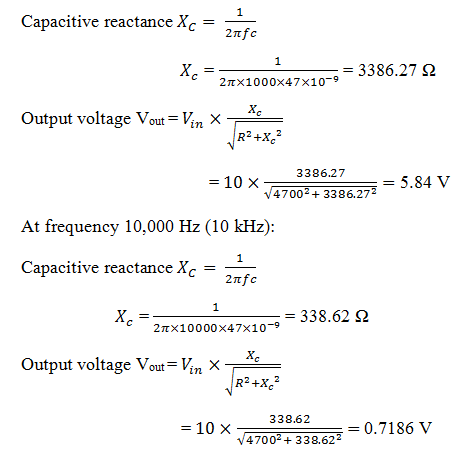
Con esto podemos decir claramente que cuando la frecuencia aumenta el capacitivo la reactancia disminuye No solo disminuye la reactancia capacitiva sino también la tensión de salida. Del ejemplo anterior se observa que la reactancia capacitiva se reduce de 3386,27 ohmios a 338,62 ohmios, mientras que la tensión de salida disminuyó de 5,84 voltios a 0,718 voltios con el aumento de la frecuencia de 1 kHz a 10 kHz.

Respuesta de frecuencia del filtro de paso bajo

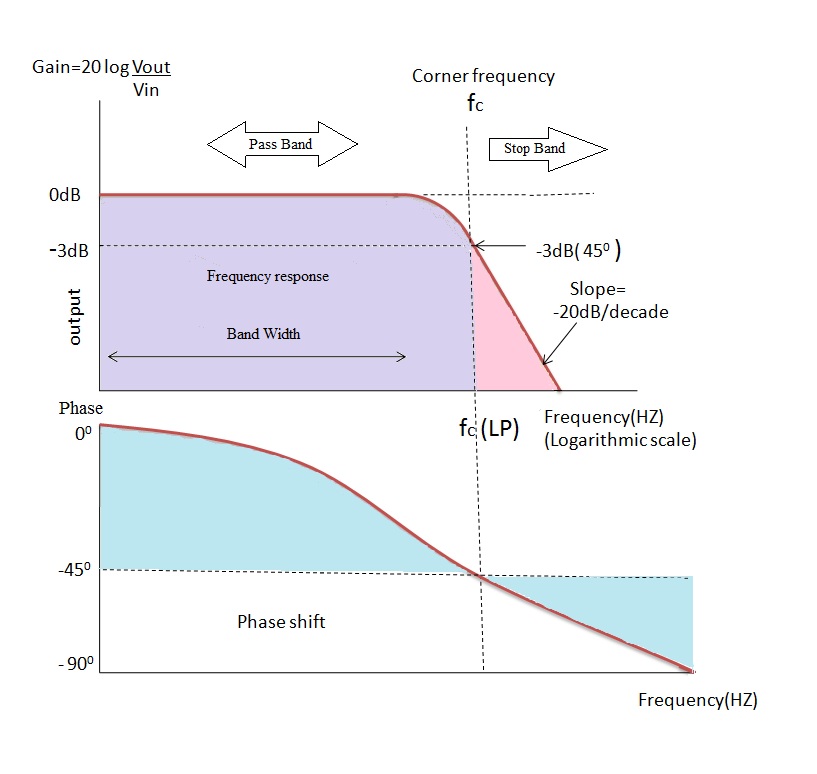
Desde la introducción a los filtros ya vimos que la magnitud | H (jω) | del filtro se toma como la ganancia del circuito. Esta ganancia se mide como 20 log (Vout/Vin) y para cualquier circuito RC el ángulo de la pendiente ‘roll-off’ es de-20 dB/década es el mismo.

La banda de frecuencias debajo del La región de corte se denomina «Banda de paso» y la banda de frecuencias después de la frecuencia de corte se denomina «Banda de detención». De la trama se puede observar que la banda de paso es el ancho de banda del filtro.

De esta gráfica queda claro que hasta la frecuencia de corte la ganancia es constante porque la tensión de salida es proporcional al valor de frecuencia en las bajas frecuencias. Esto se debe a la reactancia capacitiva que actúa como circuito abierto a bajas frecuencias y permite la máxima corriente a través del circuito para altas frecuencias. El valor de la reactancia capacitiva es muy alto a bajas frecuencias, por lo que tiene mayor capacidad de bloquear el flujo de corriente a través del circuito.

Una vez que alcanza el valor de frecuencia de corte, el voltaje de salida disminuye gradualmente y llega a cero. La ganancia también disminuye junto con el voltaje de salida. Después de la frecuencia de corte, la respuesta de la pendiente del circuito alcanzará el punto de caída, que ocurre a-20 dB/década.

Esto se debe principalmente al aumento de la frecuencia, cuando la frecuencia aumenta el capacitivo el valor de la reactancia disminuye y, por lo tanto, disminuye la capacidad de bloquear la corriente a través del condensador. Cuando aumenta la corriente a través del circuito y debido a la capacitancia limitada del condensador, el circuito actúa como cortocircuito. Por lo tanto, la tensión de salida del filtro es cero a altas frecuencias.

La única manera de evitar este problema es elegir los rangos de frecuencia hasta los cuales estas resistencias y capacitores pueden resistir. Los valores del condensador y la resistencia juegan el papel principal porque de estos valores solo depende la frecuencia de corte ‘fc’. Si los rangos de frecuencia están dentro del rango de frecuencia de corte, entonces podemos superar el problema del cortocircuito.

Este punto de corte ocurrirá cuando el valor de resistencia y el valor de reactancia capacitiva coincidan, lo que significa la suma de vectores del resistencia y capacitancia reactiva son iguales. Eso es cuando R = Xc y en esta situación la señal de entrada se atenúa en-3dB/década.

Esta atenuación es aproximadamente del 70,7% de la señal de entrada. El tiempo necesario para cargar y descargar las placas del el condensador varía según la onda sinusoidal. Debido a esto, el ángulo de fase (ø) de la señal de salida se retrasa detrás de la señal de entrada después de la frecuencia de corte. En la frecuencia de corte, la señal de salida está desfasada-45 °.

Si la entrada la frecuencia del filtro aumenta el ángulo de retraso de la señal de salida del circuito aumenta. Simplemente para el mayor valor de frecuencia, el circuito está más desfasado.

El condensador tiene más tiempo para cargar y descargar las placas a bajas frecuencias porque el tiempo de conmutación de la onda sinusoidal es mayor. Pero con el aumento de la frecuencia, el tiempo necesario para pasar al siguiente pulso disminuye gradualmente. Debido a esto, se producen variaciones de tiempo que conducen al desplazamiento de fase de la onda de salida.

La frecuencia de corte de un filtro de paso bajo pasivo depende principalmente de los valores de resistencia y condensador utilizados en el filtro del circuito.-off frequencyis inversamente proporcional a los valores de resistor y condensador. La frecuencia de corte de un filtro de paso bajo pasivo se da como

fC = 1/(2πRC)

El desplazamiento de fase de un el filtro pasivo de paso bajo se da como

Cambio de fase (ø) =-tan-1 (2πfRc)

Constante de tiempo (τ)

Como ya vimos, el tiempo que tarda el condensador en cargar y descargar las placas con respecto a la onda sinusoidal de entrada da como resultado la diferencia de fase. La resistencia y el condensador en conexión en serie producirán este efecto de carga y descarga.

La constante de tiempo de un circuito RC en serie se define como el tiempo que toma el capacitor para cargar hasta 63.2% del valor final valor de estado y también se define como el tiempo que tarda el condensador en descargar al 36.8% del valor de estado estacionario. Esta constante de tiempo se representa con el símbolo ‘τ’.

La relación entre la constante de tiempo y la frecuencia de corte es la siguiente

Constante de tiempo τ = RC = 1/2πfc y ωc = 1/τ = 1/RC

También podemos reescribir en términos de frecuencia de corte como

Con esto podemos decir que la salida del filtro depende de las frecuencias aplicadas en la entrada y en la constante de tiempo.

Passive low pass filter example2

Calculemos la frecuencia de corte de un filtro de paso bajo que tiene una resistencia de 4.7k y una capacitancia de 47nF.

Sabemos que la ecuación para la frecuencia de corte es

fc = 1/2πRC = 1/(2π x 4700 x 47 x 10-9) = 720 Hz

Segundo orden Filtro pasivo de paso bajo

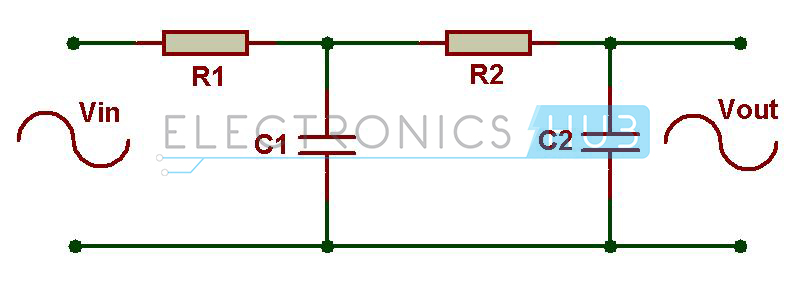
El filtro RC de paso bajo de segundo orden se puede obtener simplemente agregando una etapa más al filtro de paso bajo de primer orden. Este filtro da una pendiente de-40dB/década o-12dB/octava y un filtro de cuarta orden da una pendiente de-80dB/octava y así sucesivamente.

Filtro de paso bajo pasivo La ganancia en la frecuencia de corte es dado como

A = (1/√2) n

Donde n es el orden o número de etapas

La frecuencia de corte del filtro de paso bajo de segundo orden se da como

fc = 1/(2π√ (R1C1R2C2))

Filtro de paso bajo de segundo orden La frecuencia de-3dB se da como

f (-3dB) = fc √ (2 (1/n)-1)

Donde fc es la frecuencia de corte yn es el número de etapas y ƒ-3dB es la frecuencia de banda de paso de-3dB.

Resumen del filtro de paso bajo

El filtro de paso bajo es compuesto por una resistencia y un condensador. No solo el condensador sino cualquier componente reactivo con resistencia proporciona un filtro de paso bajo. Es un filtro que permite solo bajas frecuencias y atenúa altas frecuencias. Las frecuencias por debajo de la frecuencia de corte se denominan frecuencias de banda de paso y las frecuencias superiores a la frecuencia de corte se denominan frecuencias de banda de parada. La banda de paso es el ancho de banda del filtro.

La frecuencia de corte del filtro dependerá de los valores de los componentes elegidos para el diseño del circuito. La frecuencia de corte se puede calcular utilizando la siguiente fórmula.

fC = 1/(2πRC)

Se toma la ganancia del filtro como la magnitud del filtro y la ganancia pueden calcularse usando la fórmula 20 log (Vout/Vin). La salida del filtro es constante hasta que los niveles de frecuencia alcanzan la frecuencia de corte.

En la frecuencia de corte, la señal de salida es 70.7% de la señal de entrada y luego la salida de frecuencia de corte disminuye gradualmente a cero. El ángulo de fase de la señal de salida retrasa la señal de entrada después de la frecuencia de corte. En la frecuencia de corte, el cambio de fase de la señal de salida es de 45 °.

Si intercambiamos las posiciones de la resistencia y el condensador en el circuito de filtro de paso bajo, entonces el circuito se comporta como filtro de paso alto.

Para las ondas de entrada sinusoidales, el circuito se comporta como un filtro de paso bajo de primer orden. El funcionamiento del filtro de primer orden es que ya hemos estudiado, pero cuando cambia el tipo de señal de entrada, entonces debe observarse lo que sucede con la salida del filtro.

Cuando cambiamos el tipo de señal de entrada para cambiar modo (ON/OFF) u otra onda cuadrada, el circuito se comporta como un integrador y se trata como sigue.

Filtro de paso bajo como circuito de conformación de onda

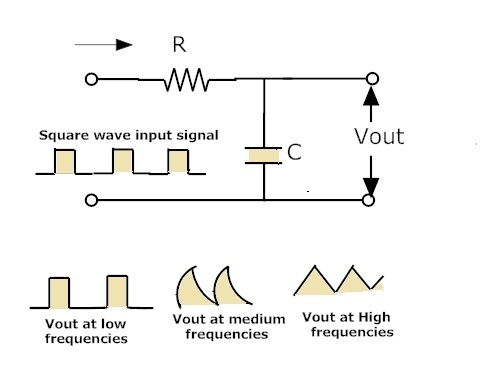
La figura anterior muestra el rendimiento del filtro para la entrada cuadrada. Cuando la entrada del filtro de paso bajo es una onda cuadrada, la salida obtenida del filtro estará en forma triangular. Esto se debe a que el condensador no puede actuar como interruptor de ENCENDIDO o APAGADO. A bajas frecuencias cuando la entrada del filtro es de onda cuadrada, la salida también estará en la onda cuadrada solamente.

Cuando la frecuencia aumenta, la salida del filtro aparece como una onda triangular. Aún así, si aumentamos la frecuencia, la amplitud de la señal de salida disminuye. La onda triangular se genera debido a la acción de los condensadores o simplemente el patrón de carga y descarga del condensador conduce a una onda triangular.

Aplicaciones del filtro de paso bajo

• El uso principal de los circuitos de filtro de paso bajo es para evitar ondulaciones de CA en la salida del rectificador. El filtro de paso bajo se usa en los circuitos de amplificación de audio.
• Al usar este filtro pasivo de paso bajo, podemos reducir directamente el ruido de alta frecuencia a un pequeño modo de perturbación en los sistemas estéreo.
• El filtro de paso bajo como integrador se puede utilizar como conformación de onda y circuitos de generación de onda debido a la fácil conversión de un tipo de señal eléctrica en otra forma.
• También se usan en circuitos demoduladores para extraer los parámetros necesarios del señales moduladas.